题目内容
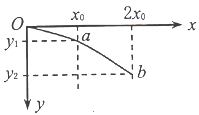
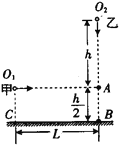
【题目】如图所示，同一竖直平面内的O1、A、B、C四点为长方形的四个顶点，水平面上的B、C两点间的距离为L，O2在A点正上方高h处，B点在A点正下方距离
处。同时将质量均为m的小球甲、乙（均可视为质点）分别从O1、O2点沿水平方向O1A和竖直方向O2A抛出，结果两球恰好在B点相遇。空气阻力不计。下列说法正确的是
A. 甲、乙抛出的初速度大小之比为
B. 两球运动过程中均处于超重状态
C. 甲、乙相遇前瞬间的动能之比为
D. 甲、乙相遇前瞬间所受重力的功率之比为1 ：2
【答案】AD
【解析】
抛体运动属于完全失重；根据平抛运动的规律计算相遇时间，求出初速度大小即可求解比值；根据运动学公式计算甲和乙达到底部竖直方向的速度，根据重力功率P＝mgvy计算功率之比；根据机械能守恒定律求解相遇前的动能，然后求解比值．
A、甲乙两球落地时间t
，则v甲
L
，对乙：
，解得：v乙
，联立解得：
，故A正确；
B、抛体运动的加速度为重力加速度，方向向下，属于完全失重，故B错误；
C、根据机械能守恒定律可得：相遇前甲的动能为：Ek1
；相遇前乙的动能为：Ek2
；所以甲、乙相遇前瞬间的动能之比为
，故C错误。
D、根据vt2﹣v02＝2ax可得：甲达到底部竖直方向的速度v1
，故甲受到的重力功率P甲＝mgv1＝mg
；乙达到底部竖直方向的速度v2
，故乙受到的重力功率P乙＝mgv2＝2mg；故甲、乙相遇前瞬间所受重力的功率之比为1：2，故D正确；
练习册系列答案
相关题目
