题目内容
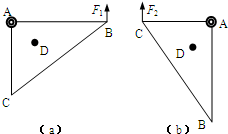 如图所示,ABC为一轻质直角形薄板,AB=0.80m、AC=0.60m,可绕过A点的水平光滑轴在竖直平面内自由转动.在薄板上D点固定一个质量为m=0.40kg的小球,用测力计竖直向上拉住B点,使AB水平,如图(a),测得拉力F1=1.0N;再用测力计竖直向上拉住C点,使AC水平,如图(b),测得拉力F2=1.0N(g取10m/s2).求:
如图所示,ABC为一轻质直角形薄板,AB=0.80m、AC=0.60m,可绕过A点的水平光滑轴在竖直平面内自由转动.在薄板上D点固定一个质量为m=0.40kg的小球,用测力计竖直向上拉住B点,使AB水平,如图(a),测得拉力F1=1.0N;再用测力计竖直向上拉住C点,使AC水平,如图(b),测得拉力F2=1.0N(g取10m/s2).求:(1)D到A点的距离AD
(2)在如图(a)情况下,撤去力F1,薄板转动过程中,C点速度的最大值vC.
分析:(1)根据力矩平衡条件列式得到D点与AC边和AB边的间距,然后根据勾股定理求解AD间距;
(2)由机械能守恒定律求出D的最大速度,然后由线速度与角速度的关系求出C的最大线速度.
(2)由机械能守恒定律求出D的最大速度,然后由线速度与角速度的关系求出C的最大线速度.
解答: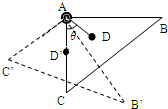 解:(1)设D点距AC边x,距AB边y.
解:(1)设D点距AC边x,距AB边y.
根据力矩平衡条件得:mg?x=F1?AB,mg?y=F2?AC,
解得x=0.2m,y=0.15m,则AD=
=0.25m;
(2)设AD连线与AC边的夹角为θ,由几何关系可知θ=53°.
根据机械能守恒定律得AD边转到竖直位置,
即转过53°时C点速度最大,
由机械能守恒定律得:mg(AD-y)=
mvD2,解得:vD=
m/s,
薄板的角速度:ω=
=4
rad/s,
则C点的最大速度:vc=ωAC=
m/s;
答:(1)D到A点的距离AD=0.25m;
(2)在如图(a)情况下,撤去力F1,薄板转动过程中,C点速度的最大值为
m/s.
 解:(1)设D点距AC边x,距AB边y.
解:(1)设D点距AC边x,距AB边y.根据力矩平衡条件得:mg?x=F1?AB,mg?y=F2?AC,
解得x=0.2m,y=0.15m,则AD=
| x2+y2 |
(2)设AD连线与AC边的夹角为θ,由几何关系可知θ=53°.
根据机械能守恒定律得AD边转到竖直位置,
即转过53°时C点速度最大,
由机械能守恒定律得:mg(AD-y)=
| 1 |
| 2 |
| 2 |
薄板的角速度:ω=
| vD |
| AD |
| 2 |
则C点的最大速度:vc=ωAC=
12
| ||
| 5 |
答:(1)D到A点的距离AD=0.25m;
(2)在如图(a)情况下,撤去力F1,薄板转动过程中,C点速度的最大值为
12
| ||
| 5 |
点评:本题关键是根据力矩平衡条件列式求解出D点的位置,然后根据机械能守恒定律或者动能定理列式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
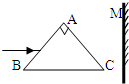 如图所示,ABC为一全反射棱镜,棱镜对不同色光折射不同,且对红光的临界角为42°,M为一与底边BC垂直的光屏,一束白光沿平行与底边BC的方向射向AB面,经AB面折射后的光线射向BC面,则( )
如图所示,ABC为一全反射棱镜,棱镜对不同色光折射不同,且对红光的临界角为42°,M为一与底边BC垂直的光屏,一束白光沿平行与底边BC的方向射向AB面,经AB面折射后的光线射向BC面,则( )| A、BC面将有色光射出 | B、光屏M上会出现色彩光带且紫光在上 | C、光屏M上会出现色彩光带且红光在上 | D、将光屏保持与BC垂直向右平移,屏上彩色光带宽度不变 |
 如图所示,ABC为一等腰直角玻璃棱镜的横截面,该玻璃临界角小于45°,一束白光平行于BC面射到AB面上,折射后能射到BC面上;该光束射出棱镜的情况是( )
如图所示,ABC为一等腰直角玻璃棱镜的横截面,该玻璃临界角小于45°,一束白光平行于BC面射到AB面上,折射后能射到BC面上;该光束射出棱镜的情况是( )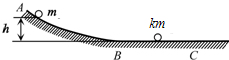 如图所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接.质量为m的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为km的小球发生碰撞,碰撞前后两小球的运动方向处于同一水平线上.
如图所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接.质量为m的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为km的小球发生碰撞,碰撞前后两小球的运动方向处于同一水平线上. 如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为
如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为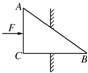 如图所示,ABC为一直角劈形物体,将其卡于孔中,劈的斜边AB=10cm,直角边AC=2cm.当用F=100N的力沿水平方向推劈时,求劈的AB面和BC面产生的推力各为多大?
如图所示,ABC为一直角劈形物体,将其卡于孔中,劈的斜边AB=10cm,直角边AC=2cm.当用F=100N的力沿水平方向推劈时,求劈的AB面和BC面产生的推力各为多大?