题目内容
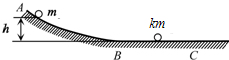 如图所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接.质量为m的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为km的小球发生碰撞,碰撞前后两小球的运动方向处于同一水平线上.
如图所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接.质量为m的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为km的小球发生碰撞,碰撞前后两小球的运动方向处于同一水平线上.(1)若两小球碰撞后粘连在一起,求碰后它们的共同速度;
(2)若两小球在碰撞过程中无机械能损失,
a.为使两小球能发生第二次碰撞,求k应满足的条件;
b.为使两小球仅能发生两次碰撞,求k应满足的条件.
分析:(1)小球下滑过程中机械能守恒,由机械能守恒定律可以求出小球到达水平面的速度;两球碰撞过程动量守恒,由动守恒定律可以求出两球的共同速度.
(2)分析出两球第二次碰撞的条件,应用动量守恒定律与机械能守恒定律分析答题.
(2)分析出两球第二次碰撞的条件,应用动量守恒定律与机械能守恒定律分析答题.
解答:解:(1)设质量为m的小球碰撞前的速度为v0,
由机械能守恒定律得:mgh=
m
①,
设两小球碰后的共同速度为V,
由动量守恒定律得:mv0=(m+km)V,②
解得:V=
;
(2)a.取水平向右方向为正方向,设碰后m与km的速度分别为v1与V1,
由动量守恒定律得:mv0=mv1+kmV1 ③,
由机械能守恒定律得:
m
=
m
+
km
④,
解得 v1=
v0⑤V1=
v0⑥
两小球若要发生第二次碰撞,需要v1<0,-v1>V1 ⑦,
由⑤⑥⑦解得:k>3; ⑧
b.对于第二次碰撞,设v2与V2分别为m与km碰后的速度,
由动量守恒定律得:m(-v1)+kmV1=mv2+kmV2 ⑨,
由机械能守恒定律得:
m
+
km
=
m
+
km
⑩,
由⑤⑥⑧⑨解得v2=
v0 (11),V2=
v0 (12),
只要满足|v2|≤V2,两球一定不会相碰(13),
由⑧(11)(12)(13)解得3<k≤5+2
;
答:(1)若两小球碰撞后粘连在一起,求碰后它们的共同速度为
;
(2)若两小球在碰撞过程中无机械能损失,
a.为使两小球能发生第二次碰撞,k应满足的条件是k>3;
b.为使两小球仅能发生两次碰撞,k应满足的条件是3<k≤5+2
.
由机械能守恒定律得:mgh=
| 1 |
| 2 |
| v | 2 0 |
设两小球碰后的共同速度为V,
由动量守恒定律得:mv0=(m+km)V,②
解得:V=
| 1 |
| k+1 |
| 2gh |
(2)a.取水平向右方向为正方向,设碰后m与km的速度分别为v1与V1,
由动量守恒定律得:mv0=mv1+kmV1 ③,
由机械能守恒定律得:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| V | 2 1 |
解得 v1=
| 1-k |
| k+1 |
| 2 |
| k+1 |
两小球若要发生第二次碰撞,需要v1<0,-v1>V1 ⑦,
由⑤⑥⑦解得:k>3; ⑧
b.对于第二次碰撞,设v2与V2分别为m与km碰后的速度,
由动量守恒定律得:m(-v1)+kmV1=mv2+kmV2 ⑨,
由机械能守恒定律得:
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| V | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| V | 2 2 |
由⑤⑥⑧⑨解得v2=
| 4k-(k-1)2 |
| (k+1)2 |
| 4(k-1) |
| (k+1)2 |
只要满足|v2|≤V2,两球一定不会相碰(13),
由⑧(11)(12)(13)解得3<k≤5+2
| 5 |
答:(1)若两小球碰撞后粘连在一起,求碰后它们的共同速度为
| ||
| k+1 |
(2)若两小球在碰撞过程中无机械能损失,
a.为使两小球能发生第二次碰撞,k应满足的条件是k>3;
b.为使两小球仅能发生两次碰撞,k应满足的条件是3<k≤5+2
| 5 |
点评:应用机械能守恒定律、动量守恒定律即可正确解题,本题的难点与解题关键是分析出碰撞条件.

练习册系列答案
相关题目
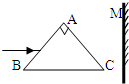 如图所示,ABC为一全反射棱镜,棱镜对不同色光折射不同,且对红光的临界角为42°,M为一与底边BC垂直的光屏,一束白光沿平行与底边BC的方向射向AB面,经AB面折射后的光线射向BC面,则( )
如图所示,ABC为一全反射棱镜,棱镜对不同色光折射不同,且对红光的临界角为42°,M为一与底边BC垂直的光屏,一束白光沿平行与底边BC的方向射向AB面,经AB面折射后的光线射向BC面,则( )| A、BC面将有色光射出 | B、光屏M上会出现色彩光带且紫光在上 | C、光屏M上会出现色彩光带且红光在上 | D、将光屏保持与BC垂直向右平移,屏上彩色光带宽度不变 |
 如图所示,ABC为一等腰直角玻璃棱镜的横截面,该玻璃临界角小于45°,一束白光平行于BC面射到AB面上,折射后能射到BC面上;该光束射出棱镜的情况是( )
如图所示,ABC为一等腰直角玻璃棱镜的横截面,该玻璃临界角小于45°,一束白光平行于BC面射到AB面上,折射后能射到BC面上;该光束射出棱镜的情况是( )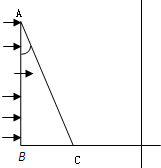 如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为
如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为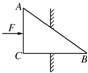 如图所示,ABC为一直角劈形物体,将其卡于孔中,劈的斜边AB=10cm,直角边AC=2cm.当用F=100N的力沿水平方向推劈时,求劈的AB面和BC面产生的推力各为多大?
如图所示,ABC为一直角劈形物体,将其卡于孔中,劈的斜边AB=10cm,直角边AC=2cm.当用F=100N的力沿水平方向推劈时,求劈的AB面和BC面产生的推力各为多大?