题目内容
【题目】一水平放置的圆盘,可以绕中心O点旋转,盘上放一个质量为m的铁块(可视为质点),轻质弹簧一端连接铁块,另一端系于O点,铁块与圆盘间的动摩擦因数为μ,如图所示.铁块随圆盘一起匀速转动,铁块距中心O点的距离为r,这时弹簧的拉力大小为F(F>μmg),g取10m/s2 , 已知铁块受到的最大静摩擦力等于滑动摩擦力,则圆盘的角速度ω大小的范围是( )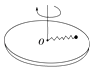
A.0<ω< ![]()
B.0≤ω≤ ![]()
C.![]() <ω<
<ω< ![]()
D.![]() ≤ω≤
≤ω≤ ![]()
【答案】D
【解析】解:当铁块匀速转动时,水平方向上铁块受弹簧拉力和静摩擦力的作用,转速较小时,静摩擦力背向圆心,则F﹣Ff=mω2r,因最大静摩擦力Ffm=μmg,得ω≥ ![]() ;
;
转速较大时,静摩擦力指向圆心,则F+Ff=mω2r,因最大静摩擦力Ffm=μmg,解得ω≤ ![]() .
.
综合以上情况可知,角速度ω的取值范围为 ![]() ≤ω≤
≤ω≤ ![]() ,D符合题意,A、B、C不符合题意.
,D符合题意,A、B、C不符合题意.
所以答案是:D.
【考点精析】本题主要考查了匀速圆周运动和向心力的相关知识点,需要掌握匀速圆周运动线速度的大小恒定,角速度、周期和频率都是恒定不变的,向心加速度和向心力的大小也都是恒定不变的,是速度大小不变而速度方向时刻在变的变速曲线运动;向心力总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小;向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时,千万不可在物体受力之外再添加一个向心力才能正确解答此题.

练习册系列答案
相关题目