��Ŀ����
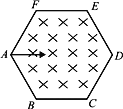
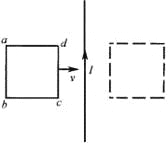
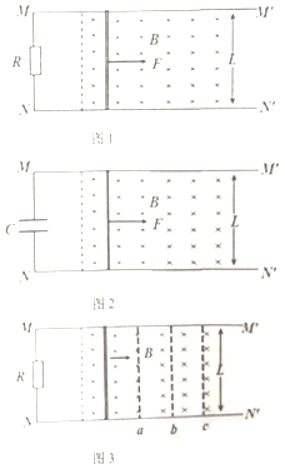
����Ŀ����ͼ��ʾ��ˮƽ�⻬��ƽ�н�������MM����MN����������L���������������ӣ�������ֵΪR����ǿ�ų���ֱ���·ֲ��ڵ������ڵĿռ��ڣ��Ÿ�Ӧǿ��ΪB������Ϊm�Ľ������ڴ�ֱ����ķ����Ͼ�ֹ�ڵ����ϣ��赼�������ĵ�������ƣ�gȡ10m/s2����
(1)��ͼ1�ڰ���ʩ��һ����ֱ���ĺ���F������������ܴﵽ������ٶ�wm�Ĵ�С��
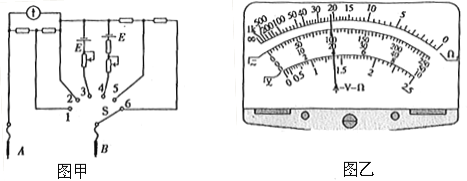
(2)������R���ɵ�����������ΪC���ڰ���ʩ��һ����ֱ���ĺ���F����ͼ2��ʾ��������������xʱ��δ�뿪�ų������������ʱ�䲻�ƣ���ʱ������δ�������������ʱ�������Ĵ�����q
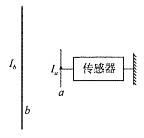
(3)���Ӻ���F��ʹ����һ���ij��ٶ������˶�����ͼ3��ʾ������ͨ��λ��aʱ���ʱ�ʾΪva��ͨ��λ��bʱ���ʱ�ʾΪvb��ע��va��vbδ֪������λ��cʱ���պþ�ֹ��a��b��b��c�ļ����ȣ��Խ���������a��b��b��c�����������У���·�в����ĵ���Eab��Ebc֮��Ϊ���
���𰸡�(1) ![]() ��(2) CBL
��(2) CBL![]() ��(3)3��1��
��(3)3��1��
��������
(1)�������ܵ��İ�������F������BIL��![]() ��
��
������������ֱ���˶�ʱ�ٶ������ƽ�������ã�F��![]() ��
��
��ã�vm��![]() ��
��
(2)�������˶����̲�����Ӧ�綯�ƣ�E��BLv��
��������������ѹ��U��E��BLv��
������ܵ��İ�������F������BIL��
�����������������q��CU��
��������I��![]() ��CBLa��
��CBLa��
�Խ���������ţ�ٵڶ����ɵã�![]()
��ã� ![]()
�����������ٶ�Ϊ����ȼ���ֱ���˶���λ�ƣ�x��![]() ��
��
��ã�t��![]() ��
��
�����������ƶ�xʱ�����������ٶȣ�v��at��![]()
��Ӧ�綯�ƣ�E��BLv��BL![]() ��
��
�������ĵ������q��CU��CE��CBL![]() ��
��
(3)ͨ���������ĵ������![]()
�������֪��a��b��b��c�ļ��d��ȣ�B��L��R��ͬ��
�����������a��b��b��c������������ͨ���������ĵ���q��ȣ�����q1��q2��
�Խ��������ɶ��������ã�
��a��b��BI1L��t1��mva��mvb��
��b��c��BI2L��t2��mvb��0��
����q1��I1��t1��q2��I2��t2��
���ڣ�q1��q2����ã�va��2vb��
�������غ㶨�ɵã�![]() mva2��
mva2��![]() mvb2+Eab��
mvb2+Eab��
![]() mvb2��E
mvb2��E![]() mvc2������vc��0��
mvc2������vc��0��
��ã�Eab��3Ebc����Eab��Ebc��3��1��