题目内容
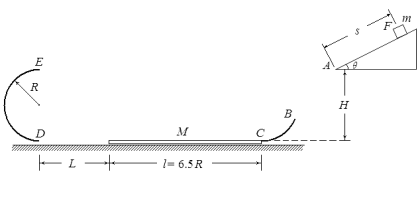
【题目】如图甲所示，一质量为m的带电小球，用绝缘细线悬挂在水平向右的匀强电场中，静止时悬线与竖直方向成θ角．小球位于A点，某时刻突然将细线剪断，经过时间t小球运动到B点（图中未画出）已知电场强度大小为E，重力加速度为g，求：
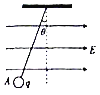
（1）小球所带的电荷量q；
（2）A、B两点间的电势差U．
【答案】（1）
；（2）
Egt2tanθ．
【解析】试题分析：（1）小球处于静止状态，分析受力，作出受力图，根据平衡条件和电场力公式求解电荷量q；（2）将细线突然剪断小球将沿细线方向做匀加速直线运动，根据牛顿第二定律求解加速度a，再根据匀变速直线运动求解位移，再计算A、B两点间的电势差U．
①静止时有
，解得 
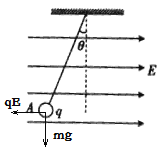
②将细线剪断后，根据牛顿第二定律可得
，解得
故
练习册系列答案
教材全解字词句篇系列答案
相关题目
【题目】（5分）为了测定滑块与水平桌面之间的动摩擦因数μ,某同学设计了如图的实验装置,其中圆弧形滑槽末端与桌面相切。第一次实验时,滑槽固定于桌面右端,末端与桌子右端M对齐,滑块从滑槽顶端由静止释放,落在水平面的P点;第二次实验时,滑槽固定于桌面左侧,测出末端N与桌子右端M的距离为L,滑块从滑槽顶端由静止释放,落在水平面的Q点,已知重力加速度为g,不计空气阻力。
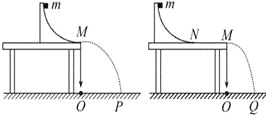
(1).实验还需要测出的物理量是(用代号表示): 。
A．滑槽的高度h |
B．桌子的高度H |
C．O点到P点的距离d1 |
D．O点到Q点的距离d2 |
E.滑块的质量m
(2).写出动摩擦因数μ的表示式是μ= 。
