题目内容
【题目】在研究机械能守恒定律时，将小球从距光滑斜轨底面h高处由静止释放，使其沿竖的光滑圆形轨道（半径为R）的内侧运动，如图所示。
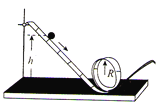
①若h =2R，小球 通过圆形轨道最高点（填“可能”或“不能”）。
②选取合适的高度h，使小球能通过圆形轨道最高点。此时若仅增大小球质量，则小球 通过圆形轨道最高点（填“能”“不能”或“不一定能”）。
③心球通过圆形轨道最低点时，对轨道的压力 重力（填“大于”“小于”或“等于”）。
【答案】①不能；②能；③大于
【解析】
试题分析：：①小球恰好能通过最高点，在最高点，由重力提供向心力，设最高点的速度为v，则有
，得
，从开始滚下到轨道最高点的过程，由机械能守恒定律得
，解得
，所以当h＜2．5R时，小球不能通过圆形轨道最高点，若
，小球不能通过圆形轨道最高点；
②选取合适的高度h．使小球能通过圆形轨道最高点，而能否通过最高点与小球的质量无关，此时若仅增大小球质量，则小球仍能通过圆形轨道最高点；
③小球通过圆形轨道最低点时，对小球受到分析，依据牛顿第二定律，则支持力与重力的合力提供向心力，即为
，解得
，那么对轨道的压力大于重力．
练习册系列答案
考前必练系列答案
相关题目
