题目内容
15. 质量均为m的A、B两物体分别自水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速,在4t0时刻两物体均静止,速度-时间图象如图所示,在下列说法正确的是( )
质量均为m的A、B两物体分别自水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速,在4t0时刻两物体均静止,速度-时间图象如图所示,在下列说法正确的是( )| A. | 摩擦力对A、B冲量大小相等 | |
| B. | F1、F2对A、B冲量大小之比为2:3 | |
| C. | F1、F2大小之比为2:1 | |
| D. | 全过程中摩擦力对A、B的做功之比为2:3 |
分析 速度图线的斜率等于加速度,根据斜率求出两个物体做匀减速直线运动的加速度大小,根据牛顿第二定律研究摩擦力关系及F1和F2大小的关系.根据图线与坐标轴所围“面积”确定出两个物体匀加速过程位移关系,求出F1和F2对A、B做功之比和全过程中摩擦力对A、B做功之比.
解答 解:A、撤去拉力后两物体做减速运动,而图象的斜率表示加速度,由图可知,两物体减速过程的加速度不相同,因此摩擦力不相等;由于运动时间相同,由I=Ft可知,摩擦力的冲量不相等,故错误;
B、根据图象的斜率表示加速度可知,匀减速运动的加速度大小分别为aA=$\frac{v_{0}}{3t_{0}}$,aB=$\frac{v_{0}}{2t_{0}}$,摩擦力大小分别为fA=maA=$\frac{m{v}_{0}}{3{t}_{0}}$,fB=maB=$\frac{v_{0}}{2t_{0}}$.对于匀加速运动过程,两物体加速度大小分别为a1=$\frac{v_{0}}{t_{0}}$,a2=$\frac{v_{0}}{2t_{0}}$,根据牛顿第二定律得,F1-fA=ma1,F2-fB=ma2,解得F1=$\frac{4mv_{0}}{3t_{0}}$,F2=$\frac{mv_{0}}{t_{0}}$,故两力的大小之比为:F1:F2=4:3;两力的冲量之比为:$\frac{{F}_{1}{t}_{0}}{{F}_{2}2{t}_{0}}$=$\frac{4}{3}×\frac{1}{2}$=$\frac{2}{3}$,故B正确;C错误;
D、由B的分析可知,摩擦力之比为:2:3,而根据v-t图象中图象的面积表示位移可知,两次运动的位移相等,根据功的公式可知,摩擦力做功之比为2:3,故D正确.
故选:BD.
点评 本题首先要掌握速度图象的两个数学方面的意义:斜率等于加速度,“面积”等于位移,其次要掌握运用牛顿定律求力和功的计算公式以及冲量的计算公式.

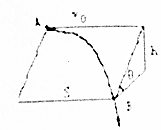 一光滑宽阔的斜面,倾角为θ,高为h,现有一小球在A处以水平速度v0射出,最后从B处离开斜面,下列说法正确的是( )
一光滑宽阔的斜面,倾角为θ,高为h,现有一小球在A处以水平速度v0射出,最后从B处离开斜面,下列说法正确的是( )| A. | 小球的运动轨迹为抛物线 | |
| B. | 小球的加速度为gsinθ | |
| C. | 小球到达B点的时间为$\frac{1}{sinθ}\sqrt{\frac{2h}{g}}$ | |
| D. | 小球到达B点的水平方向位移s=$\frac{{v}_{0}}{sinθ}\sqrt{\frac{2h}{g}}$ |
| A. | 汽车转弯时要限定速度 | |
| B. | 转动的砂轮半径不能做得太大 | |
| C. | 在修筑铁路时,转弯处轨道的内轨要低于外轨 | |
| D. | 离心水泵工作时.利用离心作用将液体从叶轮中心被甩向叶轮外缘 |
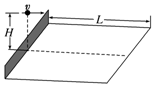 如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H 处,将球以速度 v 沿垂直球网的方向击出,球刚好落在底线上.已知底线到网的距离为 L,重力加速度取g,将球的运动视做平抛运动,下列表述正确的是( )
如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H 处,将球以速度 v 沿垂直球网的方向击出,球刚好落在底线上.已知底线到网的距离为 L,重力加速度取g,将球的运动视做平抛运动,下列表述正确的是( )| A. | 球的速度 v 等于 L$\sqrt{\frac{g}{2H}}$ | |
| B. | 球从击出至落地所用时间为$\sqrt{\frac{H}{g}}$ | |
| C. | 球从击球点至落地点的位移等于L | |
| D. | 球从击球点至落地点的位移与球的质量有关 |
| A. | 电动势随着外电路电阻增大而增大 | |
| B. | 在闭合电路中,电源电动势在数值上一定等于内外电压之和 | |
| C. | 在闭合电路中,并联在电源两端电压表的读数等于电源的电动势 | |
| D. | 电源的电动势等于电源没有接入电路时两极间的电压,所以当电源接入电路时,电动势将发生变化 |
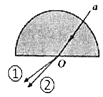 如图a光是一束由两种色光组成的复色光,射向半圆玻璃砖的圆心O,折射后由于色散分成①、②两束色光.下列说法正确的是( )
如图a光是一束由两种色光组成的复色光,射向半圆玻璃砖的圆心O,折射后由于色散分成①、②两束色光.下列说法正确的是( )| A. | 改变a光入射的角度,①光会在半圆玻璃砖直径平面下消失,②光不会消失 | |
| B. | ①光在玻璃砖中的传播速度大于②光在玻璃砖中的传播速度 | |
| C. | ①光的频率小于②光的频率 | |
| D. | 若用相同装置做双缝干涉实验,观察到①光条纹间距将比②光的小 |
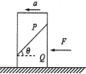 如图所示,质量均为m的两个木块P、Q叠放在水平地面上,P、Q接触面的倾角为θ,现在Q上加一水平推力F,使P、Q保持相对静止一起向左做加速直线运动,下列说法正确的是( )
如图所示,质量均为m的两个木块P、Q叠放在水平地面上,P、Q接触面的倾角为θ,现在Q上加一水平推力F,使P、Q保持相对静止一起向左做加速直线运动,下列说法正确的是( )| A. | 物体Q对地面的压力为mg | |
| B. | 若Q与地面间的动摩擦因数为μ,则μ=$\frac{F}{2mg}$ | |
| C. | 若P、Q之间光滑,则加速度a=gtanθ | |
| D. | 地面与Q间的滑动摩擦力随推力F的增大而增大 |
 竖直向下的电场,长L=0.8m不可伸长的轻绳固定于O点,另一端系一质量
竖直向下的电场,长L=0.8m不可伸长的轻绳固定于O点,另一端系一质量 的带电量
的带电量 的小球。拉起小球至绳水平后在A点无初速度释放,当小球运动至O点的正下方B点时绳恰好断裂,小球继续运动并垂直打在同一竖直平面且与水平面成
的小球。拉起小球至绳水平后在A点无初速度释放,当小球运动至O点的正下方B点时绳恰好断裂,小球继续运动并垂直打在同一竖直平面且与水平面成 、无限大的挡板MN上的C点,试求:
、无限大的挡板MN上的C点,试求:
 如图所示,在同一条电场线上有A、B两点,将q=6×10-6C的正点电荷由A移到B点,电场力做功3.0×10-5J,电势能减小(选填“增大”、“减小”或“不变”)
如图所示,在同一条电场线上有A、B两点,将q=6×10-6C的正点电荷由A移到B点,电场力做功3.0×10-5J,电势能减小(选填“增大”、“减小”或“不变”)