题目内容
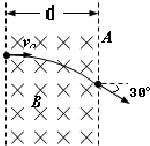
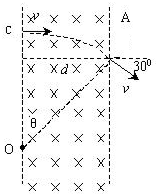
如图所示,一个电子(电量为e)以速度v0垂直射入磁感应强度为B,宽为d的匀强磁场中,穿出磁场的速度方向与电子原来的入射方向的夹角为30°,(电子重力忽略不计)求:
(1)标出电子在磁场中的轨迹的圆心O
(2)求电子在磁场中的轨道半径是多少?
(3)电子的质量是多少?
(4)电子穿过磁场的时间是多少?
(1)标出电子在磁场中的轨迹的圆心O
(2)求电子在磁场中的轨道半径是多少?
(3)电子的质量是多少?
(4)电子穿过磁场的时间是多少?

(1)电子在磁场中运动,只受洛伦兹力作用,故其轨迹是圆弧的一部分,又因为F洛⊥v,故圆心在电子穿入和穿出磁场时受到洛伦兹力指向的交点上,设圆心为O点.如图所示.
(2)由几何知识可知,圆心角θ=30°,OC为半径r,则得
r=
=2d
(3)又由qvB=
得
得m=
(4)电子穿过磁场的时间是t=
T=
T
由于T=
,故t=
答:(1)标出电子在磁场中的轨迹的圆心O如图;(2)电子在磁场中的轨道半径是2d;(3)电子的质量是
;(4)电子穿过磁场的时间是
.
(2)由几何知识可知,圆心角θ=30°,OC为半径r,则得
r=
| d |
| sin30° |
(3)又由qvB=
| mv2 |
| r |
得m=
| 2dBe |
| v0 |
(4)电子穿过磁场的时间是t=
| 30° |
| 360° |
| 1 |
| 12 |
由于T=
| 2πm |
| eB |
| πm |
| 6Be |
答:(1)标出电子在磁场中的轨迹的圆心O如图;(2)电子在磁场中的轨道半径是2d;(3)电子的质量是
| 2dBe |
| v0 |
| πm |
| 6Be |


练习册系列答案
相关题目