题目内容
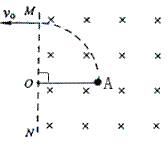
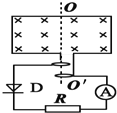
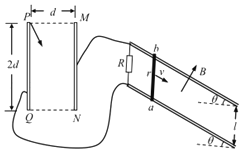
【题目】如图，一对竖直平行放置的金属极板PQ、MN间距为d、板长为2d。两极板通过导线分别连接一对金属导轨。两导轨的间距为l，平行固定在倾角为θ的斜面上，顶端连接阻值为R的电阻。一金属棒ab质量为m、电阻r＝
，水平放置在导轨上，构成闭合回路。导轨所在区域充满匀强磁场，磁感应强度大小为B，方向垂直于斜面向上。ab棒沿导轨下滑的速度大小为v时，恰好保持匀速。此时，从PQ板的上端P将一带电小球以大小为E的初动能射入极板间，结果小球沿直线PN运动，到N点射出时动能为4Ek．已知导轨足够长且可忽略空气阻力，重力加速度大小为g。
（1）求ab棒与导轨间的动摩擦因数；
（2）求带电小球的质量m0和电荷量q；
（3）若将该带电小球改为从MN板的上端M以相同的初动能Ek沿MQ连线方向射入极板间，求带电小球从极板间射出时的位置和动能。
【答案】（1）
（2）带电小球的质量为
，电荷量为
；（3）若将该带电小球改为从MN板的上端M以相同的初动能Ek沿MQ连线方向射入极板间，带电小球从极板间射出时的位置在N点左侧与N点的距离为
，动能为
【解析】
（1）ab棒匀速下滑，根据平衡条件可得：mgsinθ＝μmgcosθ+BIl，根据闭合电路的欧姆定律可得
解得：μ＝tanθ﹣
。
（2）金属板间的电压U＝IR，带电小球从P到N过程中根据动能定理可得：m0g2d+qU＝4Ek﹣Ek
根据小球沿直线运动，可知力的大小满足：
,解得带电小球的质量和电荷量各为：
（3）带电小球从P运动的N点的过程中，经过时间为t，取水平向右为正方向，则在水平方向有：
,水平方向有：
，根据初末动能的关系可得：
，带电小球从M沿MQ连线方向射入，根据竖直方向运动可得，同样经过时间t后从极板间射出，有：
，
，联立解得水平位移为
，即小球从极板间射出的位置在N点左侧与N点的距离为 ，小球在极板间运动过程中根据动能定理可得：
，解得小球从极板间射出时的动能为E′k＝
。
