题目内容
【题目】如图所示,在竖直平面内建立直角坐标系xOy,该平面内有AM、BM、CM三条光滑固定轨道,其中A、C两点处于同一个圆上,C是圆上任意一点,A、M分别为此圆与y、x轴的切点。B点在y轴上且∠BMO=60°,O′为圆心。现将a、b、c三个小球分别从A、B、C点同时由静止释放,它们将沿轨道运动到M点,如所用时间分别为tA、tB、tC,则tA、tB、tC大小关系是

A.tA<tC<tB
B.tA=tC=tB
C.tA=tC<tB
D.由于C点的位置不确定,无法比较时间大小关系
【答案】C
【解析】
试题分析:可以证明,从同一圆上任一点沿光滑轨道由静止滑到最低点M所用的时间都等于![]() ,所以tA=tC ,B在圆外一点,滑到M点的时间更长,tA=tC<tB ,所以tA=tC<tB,故选C。
,所以tA=tC ,B在圆外一点,滑到M点的时间更长,tA=tC<tB ,所以tA=tC<tB,故选C。

练习册系列答案
相关题目
【题目】关于在做“验证力的平行四边形定则”实验时:
(1)下列叙述正确的是( )
A.两弹簧测力计的拉力可以同时比橡皮筋的拉力大 |
B.橡皮筋的拉力是合力,两弹簧测力计的拉力是分力 |
C.两次拉橡皮筋时,需将橡皮筋结点拉到同一位置O.这样做的目的是保证两次弹簧测力计拉力的效果相同 |
D.若只增大某一只弹簧测力计的拉力大小而要保证橡皮筋结点位置不变,只需调整另一只弹簧测力计拉力的大小即可 |
(2)如图是李明和张华两位同学在做以上实验时得到的结果,其中哪一个实验比较符合实验事实?(力F′是用一只弹簧测力计拉时的图示)答: .
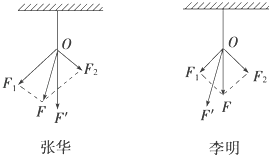
(3)在以上实验结果比较符合实验事实的一位同学中,造成误差的主要原因是:(至少写出两种情况)
答: , .