题目内容
6. 如图所示,一水平放置的圆盘,以1 rad/s的角速度绕中心轴O匀速转动,圆盘上一质量为0.4kg的铁块(可视为质点)在距中心O点50cm的位置上随圆盘一起做匀速圆周运动.已知铁块与圆盘之间的动摩擦因数为0.2,且g取10m/s2.
如图所示,一水平放置的圆盘,以1 rad/s的角速度绕中心轴O匀速转动,圆盘上一质量为0.4kg的铁块(可视为质点)在距中心O点50cm的位置上随圆盘一起做匀速圆周运动.已知铁块与圆盘之间的动摩擦因数为0.2,且g取10m/s2.求:(1)铁块所受的摩擦力大小;
(2)增大圆盘转速,若要铁块在圆盘上不发生相对滑动,则圆盘转动的最大角速度为多少?
分析 (1)根据静摩擦力提供向心力,结合牛顿第二定律求出铁块所受的摩擦力大小.
(2)当摩擦力达到最大静摩擦力,角速度达到最大,根据牛顿第二定律求出最大角速度.
解答 解:(1)根据牛顿第二定律得,f=mrω2=0.4×0.5×1N=0.2N.
(2)根据$μmg=mr{{ω}_{m}}^{2}$得,${ω}_{m}=\sqrt{\frac{μg}{r}}=\sqrt{\frac{0.2×10}{0.5}}rad/s=2rad/s$.
答:(1)铁块受到的摩擦力为0.2N.
(2)圆盘转动的最大角速度为2rad/s.
点评 解决本题的关键知道铁块做圆周运动向心力的来源,抓住临界状态,结合牛顿第二定律进行求解,基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
1.某人造地球卫星绕地球做匀速圆周运动,实施变轨后卫星的线速度减小到原来的$\frac{1}{4}$,此时卫星仍做匀速圆周运动,则( )
| A. | 卫星的向心力减小到原来的$\frac{1}{256}$ | |
| B. | 卫星的向心加速度减小到原来的$\frac{1}{16}$ | |
| C. | 卫星的绕行半径增大到原来的16倍 | |
| D. | 卫星的周期增大到原来的4倍 |
18.下列叙述中正确的有( )
| A. | 光的粒子性被光电效应和康普顿效应所证实 | |
| B. | 普朗克通过研究黑体辐射提出能量子的概念,成为量子力学的奠基人之一 | |
| C. | 放射性元素的半衰期与原子所处的化学状态和外部条件有关系 | |
| D. | 氡的半衰期为3.8天,4个氡原子核,经过7.6天后就一定只剩下一个氡原子核 |
16.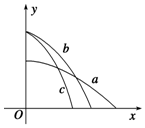 如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则 ( )
如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则 ( )
 如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则 ( )
如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则 ( )| A. | a在空中运动的时间比b的长 | B. | b和c在空中运动的时间相同 | ||
| C. | a的初速度比b的大 | D. | b的初速度比c的大 |


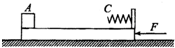 如图所示,质量为M=6kg的滑板静止在光滑水平面上,滑板的右端固定一轻弹簧.在滑板的最左端放一可视为质点的小物体A,弹簧的自由端C与A相距L=1m.弹簧下面的那段滑板是光滑的,C左侧的那段滑板是粗糙的,物体A与这段粗糙滑板间的动摩擦因数为μ=0.2,A的质量m=2kg.滑板受到水平向左恒力F作用1s后撤去,撤去水平力F时A刚好滑到C处,g取10m/s2,求:
如图所示,质量为M=6kg的滑板静止在光滑水平面上,滑板的右端固定一轻弹簧.在滑板的最左端放一可视为质点的小物体A,弹簧的自由端C与A相距L=1m.弹簧下面的那段滑板是光滑的,C左侧的那段滑板是粗糙的,物体A与这段粗糙滑板间的动摩擦因数为μ=0.2,A的质量m=2kg.滑板受到水平向左恒力F作用1s后撤去,撤去水平力F时A刚好滑到C处,g取10m/s2,求: