题目内容
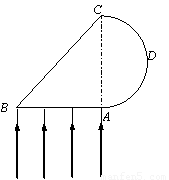
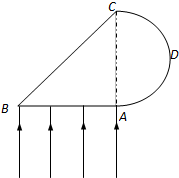 某透明物体的横截面如图所示,其中ABC为直角三角形,AB为直角边,长度为2L,∠ABC=45°,ADC为一圆弧,其圆心在AC边的中点.此透明物体的折射率为n=2.0.若一束宽度与AB边长度相等的平行光从AB边垂直射入透明物体,则光线从ADC圆弧射出区域的圆弧长度s为(不考虑经ADC圆弧反射后的光线)( )
某透明物体的横截面如图所示,其中ABC为直角三角形,AB为直角边,长度为2L,∠ABC=45°,ADC为一圆弧,其圆心在AC边的中点.此透明物体的折射率为n=2.0.若一束宽度与AB边长度相等的平行光从AB边垂直射入透明物体,则光线从ADC圆弧射出区域的圆弧长度s为(不考虑经ADC圆弧反射后的光线)( )分析:根据sinθ=
求出透明体的临界角θ为30°,当光线射到BC面上时,光线将发生全反射.从ADC圆弧射出时,作出两条边缘光线,从圆弧ADC射出的边缘光线恰好发生全反射,其入射角等于临界角,由折射率求出临界角,由几何知识求出此区域的圆弧长度s.
| 1 |
| n |
解答: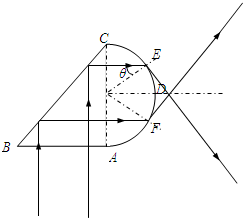 解:由sinθ=
解:由sinθ=
=
得,透明体的临界角为30°.如图,作出两条边缘光线,所求光线射出的区域为EDF.如图,从圆弧ADC射出的边缘光线对应的入射角等于材料的临界角θ,恰好发生全反射.
由几何关系得:圆弧EDF长度为s=2θ?L
故此区域的圆弧长度为:s=
.故C正确,A、B、D错误.
故选:C.
 解:由sinθ=
解:由sinθ=| 1 |
| n |
| 1 |
| 2 |
由几何关系得:圆弧EDF长度为s=2θ?L
故此区域的圆弧长度为:s=
| πL |
| 3 |
故选:C.
点评:对于几何光学中范围问题,要掌握临界角公式,求出临界角,要作出边界光线,在边界上光线往往恰好发生全反射.

练习册系列答案
相关题目
 (2013?重庆一模)某透明物体的横截面如图所示,其中ABC为直角三角形,AB为直角边,长度为2L,∠ABC=45°,ADC为一圆弧,其圆心在AC边的中点,此透明物体的折射率为n=2.0.若一束宽度与AB边长度相等的平行光从AB边垂直射入透明物体,试由光路图画出光线从ADC圆弧射出的区域,并求此区域的圆弧长度s.(不考虑经ADC圆弧反射后的光线)
(2013?重庆一模)某透明物体的横截面如图所示,其中ABC为直角三角形,AB为直角边,长度为2L,∠ABC=45°,ADC为一圆弧,其圆心在AC边的中点,此透明物体的折射率为n=2.0.若一束宽度与AB边长度相等的平行光从AB边垂直射入透明物体,试由光路图画出光线从ADC圆弧射出的区域,并求此区域的圆弧长度s.(不考虑经ADC圆弧反射后的光线) (1)关于单摆的运动有下列说法,正确的是
(1)关于单摆的运动有下列说法,正确的是