��Ŀ����
 ��ͼ��ʾ��һ�ڱڹ⻬�Ļ���ϸԲ�̶ܹ���ˮƽ�����ϣ����ڼ����ȵ���λ�ô����ֱ��о�ֹ�Ĵ�С��ͬ��С��A��B��C�������ֱ�Ϊm1=m��m2=m3=1.5m�����ǵ�ֱ����С�ڹܵ�ֱ����С�����ĵ�Բ�����ĵľ���ΪR������A�Գ��ٶ�v0�ع�˳ʱ���˶��������֮�����ײʱ�伫�̣�A��B����û�л�е����ʧ��B��C�������ܽ����һ�𣬳�ΪD����
��ͼ��ʾ��һ�ڱڹ⻬�Ļ���ϸԲ�̶ܹ���ˮƽ�����ϣ����ڼ����ȵ���λ�ô����ֱ��о�ֹ�Ĵ�С��ͬ��С��A��B��C�������ֱ�Ϊm1=m��m2=m3=1.5m�����ǵ�ֱ����С�ڹܵ�ֱ����С�����ĵ�Բ�����ĵľ���ΪR������A�Գ��ٶ�v0�ع�˳ʱ���˶��������֮�����ײʱ�伫�̣�A��B����û�л�е����ʧ��B��C�������ܽ����һ�𣬳�ΪD������1��A��B��һ����������Ե��ٶȴ�С��
��2��B��C���������һ���Թ���ˮƽ�����ѹ����С��
��3��A��B��һ��������A��D����������ʱ�䣮
��������1��A��B����ʱû�л�е����ʧ�����ض����غ�ͻ�е�������غ㣬�ֱ��г������غ㶨�ɵķ��̣����A��B��һ����������Ե��ٶȴ�С��
��2�����ݶ����غ㶨�����B��C���������һ����ٶȣ���ײ��ܶԽ�����ˮƽ����ĵ����ṩ������������ţ���˶��������B��C���������һ���Թ���ˮƽ�����ѹ����С��
��3��С����ײǰ����Բ����������Բ���˶������ݻ������ٶȵı�ֵ�����A��B����B��C������������ʱ�䣮
��A��B��һ��������D��A������AD��ͨ�����ܻ���Ϊ
������·��֮�͵����ܻ�������ʽ���A��B��һ��������A��D����������ʱ�䣮
��2�����ݶ����غ㶨�����B��C���������һ����ٶȣ���ײ��ܶԽ�����ˮƽ����ĵ����ṩ������������ţ���˶��������B��C���������һ���Թ���ˮƽ�����ѹ����С��
��3��С����ײǰ����Բ����������Բ���˶������ݻ������ٶȵı�ֵ�����A��B����B��C������������ʱ�䣮
��A��B��һ��������D��A������AD��ͨ�����ܻ���Ϊ
| 4��R |
| 3 |
����⣺��1����A��B��ײ���ٶȷֱ�Ϊv1��v2�����ݶ����غ�ͻ�е�����غ�ã�
mv0=mv1+1.5mv2
m
=
m
+
?1.5m
������ã�
v1=-
v0�����ű�ʾA����ʱ�뷵�أ���v2=
v0
��2�����������֪��BC����Ҫ��ײ����B��C���������һ����ٶ�Ϊv3�����ɶ����غ��У�
1.5mv2=3mv3
�ã�v3=
v2=
v0
��ܶ�����ˮƽ�����ѹ��N�������ṩD��������Բ���˶���������������ţ�ٵڶ����ɵã�
N=3m?
=
��
��ţ�ٵ������ɵ�֪��B��C���������һ���Թ���ˮƽ�����ѹ����С��
N��=N=
��
��3��A��B����B��ʱ��t1��C�������پ�ʱ��t2��D��A����
t1=
=
��A��B��һ��������D��A������
v3t2+|v1|?(t1+t2)=
�ã�t2=
��A��B��һ��������A��D����������ʱ��tΪ��
t=t1+t2=
��
��1��A��B��һ����������Ե��ٶȴ�С�ֱ�Ϊ
v0��
v0��
��2��B��C���������һ���Թ���ˮƽ�����ѹ����СΪ
��
��3��A��B��һ��������A��D����������ʱ��Ϊ
��
mv0=mv1+1.5mv2
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
������ã�
v1=-
| 1 |
| 5 |
| 4 |
| 5 |
��2�����������֪��BC����Ҫ��ײ����B��C���������һ����ٶ�Ϊv3�����ɶ����غ��У�
1.5mv2=3mv3
�ã�v3=
| 1 |
| 2 |
| 2 |
| 5 |
��ܶ�����ˮƽ�����ѹ��N�������ṩD��������Բ���˶���������������ţ�ٵڶ����ɵã�
N=3m?
| ||
| R |
12m
| ||
| 25R |
��ţ�ٵ������ɵ�֪��B��C���������һ���Թ���ˮƽ�����ѹ����С��
N��=N=
12m
| ||
| 25R |
��3��A��B����B��ʱ��t1��C�������پ�ʱ��t2��D��A����
t1=
| 2��R |
| 3v2 |
| 5��R |
| 6v0 |
��A��B��һ��������D��A������
v3t2+|v1|?(t1+t2)=
| 4��R |
| 3 |
�ã�t2=
| 35��R |
| 18v0 |
��A��B��һ��������A��D����������ʱ��tΪ��
t=t1+t2=
| 25��R |
| 9v0 |
��
��1��A��B��һ����������Ե��ٶȴ�С�ֱ�Ϊ
| 1 |
| 5 |
| 4 |
| 5 |
��2��B��C���������һ���Թ���ˮƽ�����ѹ����СΪ
12m
| ||
| 25R |
��3��A��B��һ��������A��D����������ʱ��Ϊ
| 25��R |
| 9v0 |
������������AB�������ǵ�����ײ��û�л�е����ʧ�����������غ�Ͷ����غ㣮�����л��漰�������⣬����λ�ƹ�ϵ�о�ʱ�䣬�dz��õķ�����

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��ͼ��ʾ��һ�ڱڹ⻬��ϸ����ɰ뾶R=0.4m�İ�Բ�ι��CD����ֱ���ã������ھ��Դ���С��ֱ����ˮƽ�������ֱ��Բ�����C��������ã�����ˮƽ����ϵĵ����������ֱǽ��������B��Ϊ���ɵ���Ȼ״̬��������һ����Ϊm=0.8kg��С��ѹ�����ɵ�A����Ȼ��С���ɾ�ֹ�ͷţ�С���˶���C����Թ����ѹ��F1=58N��ˮƽ�����BΪ�߽磬���AB�γ�Ϊx=0.3m����С��Ķ�Ħ������Ϊ��=0.5���Ҳ�BC�ι⻬����g=10m/s2��
��ͼ��ʾ��һ�ڱڹ⻬��ϸ����ɰ뾶R=0.4m�İ�Բ�ι��CD����ֱ���ã������ھ��Դ���С��ֱ����ˮƽ�������ֱ��Բ�����C��������ã�����ˮƽ����ϵĵ����������ֱǽ��������B��Ϊ���ɵ���Ȼ״̬��������һ����Ϊm=0.8kg��С��ѹ�����ɵ�A����Ȼ��С���ɾ�ֹ�ͷţ�С���˶���C����Թ����ѹ��F1=58N��ˮƽ�����BΪ�߽磬���AB�γ�Ϊx=0.3m����С��Ķ�Ħ������Ϊ��=0.5���Ҳ�BC�ι⻬����g=10m/s2�� ��ͼ��ʾ��һ�ڱڹ⻬��ϸ����ɰ뾶ΪR=0.4m�İ�Բ�ι��CD����ֱ���ã����ھ��Դ���С���ֱ����ˮƽ�������ֱ��Բ�����C��������ã�����ˮƽ����ϵĵ����������ֱǽ��������B��Ϊ���ɵ���Ȼ״̬����һ������Ϊm=0.8kg��С����ڵ��ɵ��Ҳ�������������С���ѹ��������A����Ȼ��С���ɾ�ֹ�ͷţ�С���˶���C����Թ����ѹ��ΪF1=58N��ˮƽ�����B��Ϊ�磬���AB�γ�Ϊx=0.3m����С��Ķ�Ħ������Ϊ��=0.5���Ҳ�BC�ι⻬��g=10m/s2����
��ͼ��ʾ��һ�ڱڹ⻬��ϸ����ɰ뾶ΪR=0.4m�İ�Բ�ι��CD����ֱ���ã����ھ��Դ���С���ֱ����ˮƽ�������ֱ��Բ�����C��������ã�����ˮƽ����ϵĵ����������ֱǽ��������B��Ϊ���ɵ���Ȼ״̬����һ������Ϊm=0.8kg��С����ڵ��ɵ��Ҳ�������������С���ѹ��������A����Ȼ��С���ɾ�ֹ�ͷţ�С���˶���C����Թ����ѹ��ΪF1=58N��ˮƽ�����B��Ϊ�磬���AB�γ�Ϊx=0.3m����С��Ķ�Ħ������Ϊ��=0.5���Ҳ�BC�ι⻬��g=10m/s2���� ��ͼ��ʾ��һ�ڱڹ⻬��Բ�棬����OO������ֱ�ģ�����O���·�����Ϊ2��������������ͬ��С��A��B������Ϊ�ʵ㣩��Բ���ڱ����ز�ͬ��Բ����˶������У�������
��ͼ��ʾ��һ�ڱڹ⻬��Բ�棬����OO������ֱ�ģ�����O���·�����Ϊ2��������������ͬ��С��A��B������Ϊ�ʵ㣩��Բ���ڱ����ز�ͬ��Բ����˶������У������� ��2010?����ģ�⣩��ͼ��ʾ��һ�ڱڹ⻬��Բ����խ�۹̶���ˮƽ�����ϣ����ڱ˴˼����ȵ� A��B��C��λ�ô����ֱ��о�ֹ�Ĵ�С��ͬ�ĵ���С��m1��m2��m3��С����۱ڸպýӴ�������m1�Գ��ٶ�v0�ز�˳ʱ���˶�����֪����������ֱ�Ϊm1=m��m2=m3=2m��С�����ĵ�Բ�����ĵľ���ΪR�������֮�����ײʱ�伫�̣���ײ��û��������ʧ����
��2010?����ģ�⣩��ͼ��ʾ��һ�ڱڹ⻬��Բ����խ�۹̶���ˮƽ�����ϣ����ڱ˴˼����ȵ� A��B��C��λ�ô����ֱ��о�ֹ�Ĵ�С��ͬ�ĵ���С��m1��m2��m3��С����۱ڸպýӴ�������m1�Գ��ٶ�v0�ز�˳ʱ���˶�����֪����������ֱ�Ϊm1=m��m2=m3=2m��С�����ĵ�Բ�����ĵľ���ΪR�������֮�����ײʱ�伫�̣���ײ��û��������ʧ����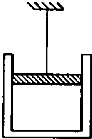 ��ͼ��ʾ��һ�ڱڹ⻬�ĵ������ף��û������һ�� �����Ŀ�������ϸ��������װ����������������Χ�����¶ȱ��ֲ��䣬������ѹǿ���ͣ�����˵����ȷ���ǣ�������
��ͼ��ʾ��һ�ڱڹ⻬�ĵ������ף��û������һ�� �����Ŀ�������ϸ��������װ����������������Χ�����¶ȱ��ֲ��䣬������ѹǿ���ͣ�����˵����ȷ���ǣ�������