题目内容
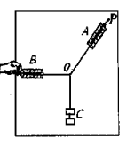
如图所示，两个质量相等而粗糙程度不同的物体m1和m2，分别固定在一细棒的两端，放在一倾角为α的斜面上，设m1和m2与斜面的摩擦因数为μ1和μ2，并满足tanα=
，细棒的质量不计，与斜面不接触，试求两物体同时有最大静摩擦力时棒与斜面上最大倾斜线AB的夹角θ的余弦值（最大静摩擦力依据滑动摩擦力公式计算）
| μ1μ2 |
系统处于平衡时，两物体所受轻杆的作用等值反向，沿斜面方向物体受力平衡，矢量关系如图：
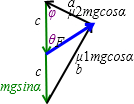
在力矢量三角形中运用余弦定理：
b2=（2c）2+a2-4accosφ
cosφ=
sinφ=
a、b、c表示各力如图中所对应，
又由余弦定理：（
）2=a2+c2-2accosφ
sin2θ=
=1-
则cosθ=
代入abc的值得：cosθ=
答：最大倾斜线AB的夹角θ的余弦值为：cosθ=
．
在力矢量三角形中运用余弦定理：
b2=（2c）2+a2-4accosφ
cosφ=
| 4c2+a2-b2 |
| 4ca |
sinφ=
| ||
| 4ac |
a、b、c表示各力如图中所对应，
又由余弦定理：（
| asinφ |
| sinθ |
sin2θ=
| a2sin2φ |
| a2+c2-2accosφ |
| (a2-b2)2 |
| 8c2(a2+c2-2c2) |
则cosθ=
| a2-b2 | ||
|
代入abc的值得：cosθ=
| μ1+μ2 | ||
2
|
答：最大倾斜线AB的夹角θ的余弦值为：cosθ=
| μ1+μ2 | ||
2
|
练习册系列答案
世纪百通期末金卷系列答案
相关题目
