题目内容
如图所示,一根轻绳跨过两个轻质光滑定滑轮O1、O2,一端与一小球连接,另一端与套在足够长的光滑固定直杆上的小滑块连接,球与滑块的质量均为m,直杆与水平面间的夹角为θ=60°,且与两个定滑轮在同一竖直平面内,直杆上的C点与两个定滑轮均在同一高度,C点到定滑轮O1的距离为L,小球运动过程中不会与其他物体相碰.缓缓释放滑块,当系统平衡时,滑块离开C点的距离为______.若将滑块从C点由静止释放,则滑块下滑距离为L时,滑块的速度大小为______.


当左边绳子竖直时球与滑块对绳子的拉力均为mg,拉力相等,系统平衡,
由几何知识知C下滑的离开C点的距离为2L;
当滑块下滑距离为L时,设其速度大小为vA,
此时小球B的速度大小为vB,则:vB=vAcosθ
小物块A下滑过程中系统的机械能守恒,由机械能守恒定律得:
mgLsinθ=
mvB2+
mvA2
解得:v=
;
故答案为:2L,
.
由几何知识知C下滑的离开C点的距离为2L;
当滑块下滑距离为L时,设其速度大小为vA,
此时小球B的速度大小为vB,则:vB=vAcosθ
小物块A下滑过程中系统的机械能守恒,由机械能守恒定律得:
mgLsinθ=
| 1 |
| 2 |
| 1 |
| 2 |
解得:v=
|
故答案为:2L,
|

练习册系列答案
相关题目





 ,现在保持A读数不变化,减小
,现在保持A读数不变化,减小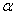 角,要使结点仍在O处,可采用的办法是( )
角,要使结点仍在O处,可采用的办法是( )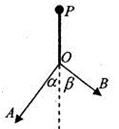
 角
角