题目内容
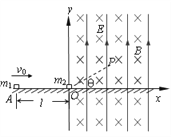
【题目】如图所示，直角坐标系Oxy位于竖直平面内，x轴与绝缘的水平面重合，在y轴右方有垂直纸面向里的匀强磁场和竖直向上的匀强电场．质量为m2=8×10-3kg的不带电小物块静止在原点O，A点距O点L=0.045m，质量m1=1×10-3kg的带电小物块以初速度v0=0.5m/s从A点水平向右运动，在O点与m2发生正碰并把部分电量转移到m2上，碰撞后m2的速度为0.1m/s，此后不再考虑m1、m2间的库仑力．已知电场强度E=40N/C，小物块m1与水平面的动摩擦因数为μ=0.1，取g=10m/s2，求：
（1）碰后m1的速度；
（2）若碰后m2做匀速圆周运动且恰好通过P点，OP与x轴的夹角θ=30°，OP长为Lop=0.4m，求磁感应强度B的大小；
（3）其它条件不变，若改变磁场磁感应强度的大小为B/使m2能与m1再次相碰，求B/的大小？
【答案】（1）0.4m/s，方向向左 （2）1T （3）0.25T
【解析】
试题(1)m1与m2碰前速度为v1，由动能定理
－μm1gl＝
m1v
－m1v
代入数据解得：v1＝0.4 m/s
设v2＝0.1 m/s，m1、m2正碰，由动量守恒有：
m1v1＝m1v1′＋m2v2
代入数据得：v1′＝－0.4 m/s，方向水平向左
(2)m2恰好做匀速圆周运动，所以qE＝m2g
得：q＝2×10－3C
粒子由洛伦兹力提供向心力，设其做圆周运动的半径为R，则
qv2B＝m2
轨迹如图，由几何关系有：R＝lOP
解得：B＝1 T
(3)当m2经过y轴时速度水平向左，离开电场后做平抛运动，m1碰后做匀减速运动．
m1匀减速运动至停，其平均速度为：
＝v1′＝0.2 m/s>v2＝0.1 m/s
所以m2在m1停止后与其相碰
由牛顿第二定律有：f＝μm1g＝m1a
m1停止后离O点距离：s＝
则m2平抛的时间：t＝
平抛的高度：h＝gt2
设m2做匀速圆周运动的半径为R′，由几何关系有：
R′＝h
由qv2B′＝
联立得：B′＝0.25 T
