题目内容
1. 如图所示,雪道与水平冰面在B处平滑地连接.小明乘雪橇从雪道上离冰面高度h=8m 的A处自静止开始下滑,经B处后沿水平冰面滑至C处停止.已知小明与雪橇的总质量m=70kg,用速度传感器测得雪橇在B处的速度值vB=12m/s,不计空气阻力和连接处能量损失,小明和雪橇可视为质点.g取10m/s2,问:
如图所示,雪道与水平冰面在B处平滑地连接.小明乘雪橇从雪道上离冰面高度h=8m 的A处自静止开始下滑,经B处后沿水平冰面滑至C处停止.已知小明与雪橇的总质量m=70kg,用速度传感器测得雪橇在B处的速度值vB=12m/s,不计空气阻力和连接处能量损失,小明和雪橇可视为质点.g取10m/s2,问:(1)从A到B过程中,小明与雪橇损失了多少机械能?
(2)从B到C过程中,小明所受摩擦力做了多少功?
分析 (1)机械能的损失等于初末机械能的差.
(2)从B到C过程中,只有摩擦力对小明做功,由动能定理求解摩擦力做功.
解答 解:(1)从A到B过程中,小明与雪橇损失的机械能为:
△E=mgh-$\frac{1}{2}$mvB2=70×10×8-$\frac{1}{2}$×70×122=560J
(2)从B到C过程中,由动能定理得:
小明所受摩擦力做 Wf=0-$\frac{1}{2}$mvB2=-$\frac{1}{2}$×70×122=-5040J
答:
(1)从A到B过程中,小明与雪橇损失了560J的机械能.
(2)从B到C过程中,小明所受摩擦力做了-5040J的功.
点评 本题考查功的计算是借助于动能定理求得,也可以由功的表达式W=FS,但F必须是恒力,且关键是确定在力的方向上移动的距离,计算时注意力和距离要对应.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17.质量为m的小球从高h处由静止自由下落,经时间t落地,关于重力的功率正确的是( )
| A. | 重力的功率即描述重力做功的快慢 | B. | 重力的平均功率等于$\frac{mgh}{2t}$ | ||
| C. | 落地时重力的功率等于$\frac{mgh}{t}$ | D. | 落地时重力的功率等于2mg$\sqrt{gh}$ |
18.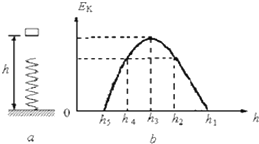 如图a所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图b所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法不正确的是( )
如图a所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图b所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法不正确的是( )
 如图a所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图b所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法不正确的是( )
如图a所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图b所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法不正确的是( )| A. | 小物体下降至高度h3时,弹簧形变量为0 | |
| B. | 小物体下落至高度h5时,加速度为0 | |
| C. | 小物体从高度h2下降到h4,弹簧的弹性势能增加了$\frac{{m}^{2}{g}^{2}}{k}$ | |
| D. | 小物体从高度h1下降到h5,弹簧的最大弹性势能为mg(h1-h5) |
9. 如图所示表示撑杆跳高运动的几个阶段:助跑、撑杆起跳、越横杆、落地(未画出).在这几个阶段中有关能量转化情况的说法,正确的是( )
如图所示表示撑杆跳高运动的几个阶段:助跑、撑杆起跳、越横杆、落地(未画出).在这几个阶段中有关能量转化情况的说法,正确的是( )
 如图所示表示撑杆跳高运动的几个阶段:助跑、撑杆起跳、越横杆、落地(未画出).在这几个阶段中有关能量转化情况的说法,正确的是( )
如图所示表示撑杆跳高运动的几个阶段:助跑、撑杆起跳、越横杆、落地(未画出).在这几个阶段中有关能量转化情况的说法,正确的是( )| A. | 助跑阶段,身体中的化学能转化为人和杆的动能 | |
| B. | 起跳时,人的动能和化学能转化为人和杆的势能 | |
| C. | 越过横杆后,人的重力势能转化为动能 | |
| D. | 落地后,人的能量消失了 |
16.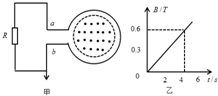 如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,b端接地,则下列说法正确的是( )
如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,b端接地,则下列说法正确的是( )
 如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,b端接地,则下列说法正确的是( )
如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,b端接地,则下列说法正确的是( )| A. | 圆形线圈中产生的感应电动势E=6V | |
| B. | 电阻R两端的电压为4.5V | |
| C. | 通过电阻R的电流为I=1.5A | |
| D. | 在0-4s时间内,b端的电势比a端的电势低 |
6.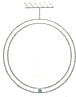 如图所示,内壁光滑的大圆管,用一细轻杆固定在竖直平面内;在管内有一小球(可视为质点)做圆周运动.下列说法正确的是( )
如图所示,内壁光滑的大圆管,用一细轻杆固定在竖直平面内;在管内有一小球(可视为质点)做圆周运动.下列说法正确的是( )
 如图所示,内壁光滑的大圆管,用一细轻杆固定在竖直平面内;在管内有一小球(可视为质点)做圆周运动.下列说法正确的是( )
如图所示,内壁光滑的大圆管,用一细轻杆固定在竖直平面内;在管内有一小球(可视为质点)做圆周运动.下列说法正确的是( )| A. | 小球通过最低点时,小球对圆管的压力向下 | |
| B. | 小球通过最高点时,小球对圆管可能无压力 | |
| C. | 细杆对圆管的作用力一定大于圆管的重力大小 | |
| D. | 细杆对圆管的作用力可能会大于圆管和小球的总重力大小 |
13.下列说法中正确的是( )
| A. | 重力势能恒大于零 | |
| B. | 重力做功的多少与参考平面的选取有关 | |
| C. | 放在地面上的物体,它的重力势能一定等于零 | |
| D. | 相对不同的参考平面,物体具有不同数值的重力势能,但并不影响研究有关重力势能 |

