Question

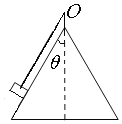
【题目】一个光滑的圆锥体固定在水平桌面上，其轴线沿竖直方向，母线与轴线之间的夹角θ=30°．一条长为L的轻绳一端固定在圆锥体的顶点O处，另一端拴着质量为m的物体（物体可看做质点），物体以角速度ω绕圆锥体的轴线作水平匀速圆周运动．

（1）当ω1=时，求绳的拉力T1；

（2）当ω2=时，求绳的拉力T2．

Answer 1

【答案】（1）（2）2mg．

【解析】

：当物体刚离开锥面时：

Tcosθ-mg=0，

由拉力与重力的合力提供向心力，则有：

解之得：

①

（1）当小球以角速度1=＜ω0时，则存在球受到斜面的支持力，因此由支持力、重力与拉力的合力提供向心力．

对球受力分析，如图所示，则有

②

T1cosθ+Nsinθ=mg ③

由②③联式解之得：

（2）当小球以角速度ω2=＞ω0时，则球只由重力与拉力的合力提供向心力，且细绳与竖直方向夹角已增大．

如图所示，则有

④

T2cosα=mg ⑤

由④⑤联式解得：T2=2mg

答：（1）当ω1=时，绳的拉力为；

（2）当ω2=时，绳的拉力为2mg．