题目内容
17. 如图所示,在竖直平面内固定有两个很靠近的同心圆轨道,A、B分别为最高点和最低点(图中未标出),外圆光滑内圆粗糙.一质量为m=0.2kg的小球从轨道的最低点以水平向右的初速度v0开始运动,球的直径略小于两圆间距,球运动的轨道半径R=0.5m,重力加速度g取10m/s2,不计空气阻力,设小球过最低点B时重力势能为零,下列说法中正确的是( )
如图所示,在竖直平面内固定有两个很靠近的同心圆轨道,A、B分别为最高点和最低点(图中未标出),外圆光滑内圆粗糙.一质量为m=0.2kg的小球从轨道的最低点以水平向右的初速度v0开始运动,球的直径略小于两圆间距,球运动的轨道半径R=0.5m,重力加速度g取10m/s2,不计空气阻力,设小球过最低点B时重力势能为零,下列说法中正确的是( )| A. | 若小球运动到最高点A时速度为0,则小球机械能一定不守恒 | |
| B. | 若小球第一次运动到最高点时速度大小为0,则v0一定等于2$\sqrt{5}$m/s | |
| C. | 若要小球不挤压内轨,则v0一定不小于5m/s | |
| D. | 若小球开始运动时初动能为1.6 J,则足够长时间后小球的机械能为1 J |
分析 内圆粗糙,小球与内圆接触时要受到摩擦力作用,要克服摩擦力做功,机械能不守恒;
外圆光滑,小球与外圆接触时不受摩擦力作用,只有重力做功,机械能守恒,应用牛顿第二定律与机械能守恒定律分析答题.
解答 解:A、若小球运动到最高点时受到为0,则小球在运动过程中一定与内圆接触,受到摩擦力作用,要克服摩擦力做功,机械能不守恒,故A正确;
B、如果内圆光滑,小球在运动过程中不受摩擦力,小球在运动过程中机械能守恒,如果小球运动到最高点时速度为0,由机械能守恒定律得:$\frac{1}{2}$mv02=mg•2R,小球在最低点时的速度${v}_{0}=2\sqrt{gR}=2\sqrt{10×0.5}m/s=2\sqrt{5}m/s$,由于内圆粗糙,小球在运动过程中要克服摩擦力做功,则小球在最低点时的速度应大于2$\sqrt{5}$m/s,故B错误;
C、小球如果不挤压内轨,则小球到达最高点速度最小时,小球的重力提供向心力,由牛顿第二定律得:mg=m$\frac{{v}^{2}}{R}$,由于小球不挤压内轨,则小球在整个运动过程中不受摩擦力作用,只有重力做功,机械能守恒,从最低点到最高点过程中,由机械能守恒定律得:$\frac{1}{2}$mv02=$\frac{1}{2}$mv2+mg•2R,解得:v0=5m/s,则小球要不挤压内轨,速度应大于等于5m/s,故C正确;
D、根据${E}_{K}=\frac{1}{2}m{v}^{2}$得小球的初速度为${v}_{0}=\sqrt{\frac{2{E}_{K}}{m}}=\sqrt{\frac{2×1.6}{0.2}}m/s=4m/s$<5m/s,则小球在运动过程中要与内轨接触,要克服摩擦力做功,机械能减少,最终小球将在轨道的下半圆内做往复运动,到达与圆心同高位置处速度为零,则小球的最终机械能为:E=mgR=0.2×10×0.5=1J,故D正确;
故选:ACD.
点评 本题综合考查了动能定理、牛顿第二定律和机械能守恒定律,综合性较强,关键是理清运动过程,抓住临界状态,运用合适的规律进行求解.

| A. | 物体的速度变化量大,加速度就一定大 | |
| B. | 物体运动的时间越长,加速度就一定越来越小 | |
| C. | 物体可能做加速度减小的加速运动 | |
| D. | 物体具有的加速度向东,所以它不可能向西运动 |
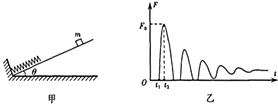 如图甲,固定斜面倾角为θ,底部挡板连一轻质弹簧.质量为m的物块从斜面上某一高度处静止释放,不断撞击弹簧,最终静止.物块所受弹簧弹力F的大小随时间t变化的关系如图乙,物块与斜面间的动摩擦因数为μ,弹簧在弹性限度内,重力加速度为g,则( )
如图甲,固定斜面倾角为θ,底部挡板连一轻质弹簧.质量为m的物块从斜面上某一高度处静止释放,不断撞击弹簧,最终静止.物块所受弹簧弹力F的大小随时间t变化的关系如图乙,物块与斜面间的动摩擦因数为μ,弹簧在弹性限度内,重力加速度为g,则( )| A. | 物块运动过程中,物块和弹簧组成的系统机械能守恒 | |
| B. | 物块运动过程中,t1到t2某时刻速度最大 | |
| C. | 物块运动过程中的最大加速度大小为$\frac{{F}_{0}-mgsinθ+μmgcosθ}{m}$ | |
| D. | 最终静止时,物块受到的重力、斜面支持力和摩擦力的合力方向沿斜面向上 |
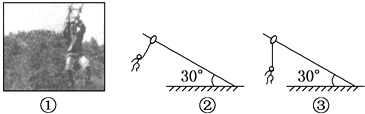
| A. | 图②的情形中,人只能匀加速下滑 | |
| B. | 图②的情形中,钢索对人的作用力大小为$\frac{\sqrt{3}mg}{2}$ | |
| C. | 图③的情形中,人匀速下滑 | |
| D. | 图③的情形中,钢索对轻环无摩擦力 |
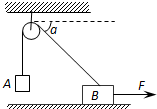 如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,(0°<α<90°)则( )
如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中,(0°<α<90°)则( )| A. | 物体A也做匀速直线运动 | B. | 物体A将竖直向上先加速后减速 | ||
| C. | 物体A将处于超重状态 | D. | 绳子对物体A的拉力保持不变 |
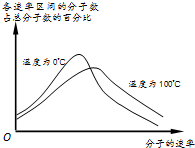 如图所示,是氧气在0℃和100℃两种不同情况下,各速率区间的分子数占总分子数的百分比与分子速率间的关系.由图可知( )
如图所示,是氧气在0℃和100℃两种不同情况下,各速率区间的分子数占总分子数的百分比与分子速率间的关系.由图可知( )| A. | 100℃的氧气,速率大的分子比例较多 | |
| B. | 具有最大比例的速率区间,0℃时对应的速率大 | |
| C. | 温度越高,分子的平均速率越大 | |
| D. | 在0℃时,也有一部分分子的速率比较大,说明气体内部有温度较高的区域 |
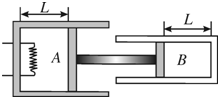 如图所示,绝热汽缸A与导热汽缸B均固定于地面,由刚性杆连接的绝热活塞与两汽缸间均无摩擦.已知两汽缸的横截面积之比SA:SB=2:1,两汽缸内均装有处于平衡状态的某理想气体,开始时两汽缸中的活塞与缸底的距离均为L,温度均为T0,压强均等于外界大气压.缓慢加热A中气体,停止加热达到稳定后,A中气体压强等于外界大气压的1.2倍.设环境温度始终保持不变,求
如图所示,绝热汽缸A与导热汽缸B均固定于地面,由刚性杆连接的绝热活塞与两汽缸间均无摩擦.已知两汽缸的横截面积之比SA:SB=2:1,两汽缸内均装有处于平衡状态的某理想气体,开始时两汽缸中的活塞与缸底的距离均为L,温度均为T0,压强均等于外界大气压.缓慢加热A中气体,停止加热达到稳定后,A中气体压强等于外界大气压的1.2倍.设环境温度始终保持不变,求