题目内容
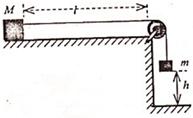
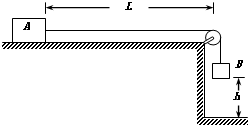 如图所示,水平平台的右端安装有定滑轮(大小忽略不计),质量M=2kg的物块A放在平台上与滑轮相距L=2.5m,物块A与平台的动摩擦因数μ=0.2.现有一轻绳跨过定滑轮,左端与物块A相连,另一端挂质量为m的物体B,绳拉直时用手托住物体B停在距离地面h=0.5m处静止不动.某时刻放开物体B,着地后物体B立即停止运动,要使物块A不撞到定滑轮,物体B的质量m应满足什么条件?(g取10m/s2)
如图所示,水平平台的右端安装有定滑轮(大小忽略不计),质量M=2kg的物块A放在平台上与滑轮相距L=2.5m,物块A与平台的动摩擦因数μ=0.2.现有一轻绳跨过定滑轮,左端与物块A相连,另一端挂质量为m的物体B,绳拉直时用手托住物体B停在距离地面h=0.5m处静止不动.某时刻放开物体B,着地后物体B立即停止运动,要使物块A不撞到定滑轮,物体B的质量m应满足什么条件?(g取10m/s2)分析:由速度位移公式求出小球落地时的速度v.根据动能定理求出s与速度v的关系.要使物块不撞到定滑轮,必须有s≤l-h,解出加速度a的范围,求出m的范围.要能拉动物块的条件:小球的重力必须大于物块所受的最大静摩擦力,再得出m的范围,再联立得到m满足的条件.
解答:解:要使A从静到动,所以mg>μMg,即m>0.4kg
设B着地时的速度为v.
从放手到B着地前,对A、B有:(mg-f)h=
(M+m)v2①
从B着地到A停在滑轮处,对A有:f(L-h)=
Mv2②
又f=μMg③
由以上三式代入已知数据解得:m=10kg
所以要使A不与滑轮相撞,则4kg<m<10kg
答:物体B的质量m应满足4kg<m<10kg.
设B着地时的速度为v.
从放手到B着地前,对A、B有:(mg-f)h=
| 1 |
| 2 |
从B着地到A停在滑轮处,对A有:f(L-h)=
| 1 |
| 2 |
又f=μMg③
由以上三式代入已知数据解得:m=10kg
所以要使A不与滑轮相撞,则4kg<m<10kg
答:物体B的质量m应满足4kg<m<10kg.
点评:本题连接体问题,运用牛顿第二定律时,由于小球与物块的加速度不同,需要采用隔离法研究.涉及距离问题,运用动能定理是通常的思路.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
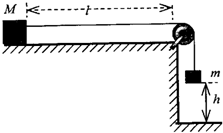 如图所示,水平平台的右端安装有滑轮,质量为M的物块放在与滑轮相距l的平台上,物块与平台间的动摩擦因数为μ现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为m的小球,绳拉直时用手托住小球使其在距地面h高处静止,重力加速度为g.设最大静摩擦力等于滑动摩擦力(g取10m/s2).
如图所示,水平平台的右端安装有滑轮,质量为M的物块放在与滑轮相距l的平台上,物块与平台间的动摩擦因数为μ现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为m的小球,绳拉直时用手托住小球使其在距地面h高处静止,重力加速度为g.设最大静摩擦力等于滑动摩擦力(g取10m/s2). 处,M与平台的动摩擦因数
处,M与平台的动摩擦因数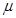 ,现有一轻绳跨过定滑轮,右端与M连,另一端挂质量
,现有一轻绳跨过定滑轮,右端与M连,另一端挂质量 物块,绳拉直时用手托住
物块,绳拉直时用手托住 ,
,