题目内容
4．
如图所示，一个人坐在小车的水平台面上，用水平力拉绕过定滑轮的细绳，使人和车以相同的加速度向右运动，水平地面光滑，则（ ）| A． | 若人的质量大于车的质量，车对人的摩擦力为0 | |
| B． | 若人的质量小于车的质量，车对人的摩擦力方向向左 | |
| C． | 若人的质量等于车的质量，车对人的摩擦力为0 | |
| D． | 不管人、车质量关系如何，车对人的摩擦力都为0 |
分析 对人和车分别受力分析，根据牛顿第二定律列方程求解．
解答 解：设绳子拉力为T，人与车间的静摩擦力为f，假设车对人的静摩擦力向左，人对车的静摩擦力向右，根据牛顿第二定律，有
T-f=ma
T+f=Ma
解得
f=$\frac{1}{2}$（M-m）a
当M=m时，无摩擦力；当M＞m时，假设成立，即车对人的静摩擦力向左；当M＜m时，摩擦力方向与假设的方向相反，即人对车的静摩擦力向左．所以BC正确，AD错误．
故选：BC．
点评 本题关键是分别对人和小车受力分析，然后根据牛顿第二定律列式求解出摩擦力的表达式分析讨论；对摩擦力方向的处理先假定一个方向，当结果为负时表示假定的方向与实际方向相反．
练习册系列答案
相关题目
17．铁路转弯处要求设计成外轨比内轨高的斜面，当火车以规定的速度通过弯道时，轮缘对内轨、外轨均无挤压．若某转弯处斜面的倾角为θ，火车的转弯半径为r，重力加速度为g，则火车通过此弯道的规定速度大小为（ ）
| A． | $\sqrt{grsinθ}$ | B． | $\sqrt{grcosθ}$ | C． | $\sqrt{grtanθ}$ | D． | $\sqrt{grcotθ}$ |
长为L=1.2m，质量为M=6kg的平板小车静止在光滑水平面上，车的左端放一质量m=2kg的木块Q（不计其大小），小木块和小车之间的动摩擦因数μ=0.15，将F=10N的水平恒力作用在木块上，使其在小车上滑行，（取g=10m/s2）．
2011年2月第七届亚冬会在哈萨克斯坦落下帷幕，中国体育代表团获得了11枚金牌的可喜成绩．如图所示，某跳台滑雪运动员从跳台边缘的O点以水平方向的速度跳出．他离开跳台时的速度为v0=8.0m/s，运动员连同滑雪板的质量为m=50kg，他落到了斜坡上的A点，斜坡与水平面的夹角为37°，O点位于斜坡上的B点的正上方，OB之间的高度为h=3.2m．忽略空气阻力的影响，重力加速度g=10m/s2．求运动员在空中飞行的时间t以及运动员落在斜坡上的速度大小v．（sin 37°=0.6）
某同学在用多用表的欧姆档测量某一电阻时，先后分别用R×1，R×10两个点阻档进行测量，三次测量所指的位置分别如图中的①②③所示，为提高测量的精确度，应该用×10档（填、），此被测电阻的阻值约为300Ω．
14．
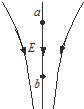如图所示为空间某一电场的电场线，a、b两点为其中一条竖直向下的电场线上的两点，该两点的高度差为h，一个质量为m、带电量为+q的小球从a点静止释放后沿电场线运动到b点时速度大小为$\sqrt{3gh}$，则下列说法中正确的有（ ）
如图所示为空间某一电场的电场线，a、b两点为其中一条竖直向下的电场线上的两点，该两点的高度差为h，一个质量为m、带电量为+q的小球从a点静止释放后沿电场线运动到b点时速度大小为$\sqrt{3gh}$，则下列说法中正确的有（ ）| A． | 质量为m、带电量为+2q的小球从a点静止释放后沿电场线运动到b点时速度大小为2$\sqrt{gh}$ | |
| B． | 质量为m、带电量为-q的小球从a点静止释放后沿电场线运动到b点时速度大小为2$\sqrt{gh}$ | |
| C． | 质量为2m、带电量为-q的小球从a点静止释放后沿电场线运动到b点时速度大小为$\sqrt{gh}$ | |
| D． | 质量为2m、带电量为-2q的小球从a点静止释放后沿电场线运动到b点时速度大小为$\sqrt{gh}$ |