题目内容

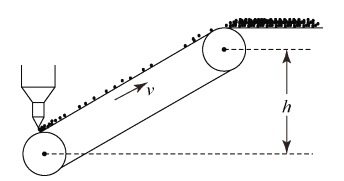
【题目】倾角θ=37°的传送带以速度v=1.0m/s顺时针转动，位于其底部的煤斗每秒钟向其输送k=4.0kg的煤屑，煤屑刚落到传送带上的速度为零，传送带将煤屑送到h=3.0m的高处，煤屑与传送带间的动摩擦因数μ=0.8，且煤屑在到达最高点前已经和传送带的速度相等。（重力加速度g=10m/s2，传送带轮子直径可忽略）求：

(1)煤屑从落到传送带开始，运动到与传送带速度相等时前进的位移和时间；

(2)传送带电机因输送煤屑而多产生的输出功率。

【答案】(1)1.25m；2.5s； (2)154W

【解析】

(1) 对煤屑，由牛顿第二定律

煤屑从落到传送带开始，运动到与传送带速度相等时前进的位移

时间

(2)设经过时间，煤屑动能增加量

重力势能增加量

摩擦产生的热量

传送带电机因输送煤屑而多产生的输出功率

练习册系列答案
相关题目

【题目】（1）某同学利用多用电表测量一个未知电阻的阻值，由于第一次选择的欧姆挡（×10），发现表针偏转角度极小。现将旋钮调至另外一档，进行第二次测量使多用电表指针指在理想位置。下面列出第二次测量的可能进行的操作：

A．将两表笔短接，并调零

B．将两表笔分别跟被测电阻的两端接触，观察指针的位置

C．将多用电表在板上旋钮调到×100档D．将多用电表面板上旋钮调到×1档

E．随即记下表盘的读数，乘以欧姆表的倍率挡，测得电阻值

根据上述有关操作，请选择合理实验步骤并按操作顺序写出_____________________。

(2)使用多用电表进行了两次测量，指针所指的位置分别如图中a、b所示。

若选择开关处在“×10Ω”的电阻档时指针位于a，则被测电阻的阻值是_____Ω．

若选择开关处在“直流电压2.5V”档时指针位于b，则 被测电压是________ V；

(3)使用完多用电表后，分别把选择开关置于______________（A、直流500V。B、交流500V 。C、OFF 填序号 ）位置。

【题目】如图，第一次，小球从粗糙的圆形轨道顶端A由静止滑下，到达底端B的速度为v1，克服摩擦力做功为W1；第二次，同一小球从底端B以v2冲上圆形轨道，恰好能到达A点，克服摩擦力做功为W2，则

A. v1可能等于v2

B. W1一定小于W2

C. 小球第一次运动机械能变大了

D. 小球第一次经过圆弧某点C的速率小于它第二次经过同一点C的速率

【题目】小明同学利用如图所示的装置来验证机械能守恒定律．A为装有挡光片的钩码，总质量为M，挡光片的挡光宽度为b，轻绳一端与A相连，另一端跨过光滑轻质定滑轮与质量为m（m<M）的重物B相连．他的做法是：先用力拉住B，保持A、B静止，测出A的挡光片上端到光电门的距离h；然后由静止释放B，A下落过程中经过光电门，光电门可测出挡光片的挡光时间t，算出挡光片经过光电门的平均速度，将其视为A下落h（h>>b）时的速度，重力加速度为g．

(1)在A从静止开始下落h的过程中，验证以A、B、地球所组成的系统机械能守恒定律的表达式为_______________________（用题目所给物理量的符号表示）；

(2)由于光电门所测的平均速度与物体A下落h时的瞬时速度间存在一个差值，因而系统减少的重力势能_________系统增加的动能（选填“大于”或“小于”）；

(3)为减小上述对结果的影响，小明同学想到了以下一些做法，其中可行的是________

A．保持A下落的初始位置不变，测出多组t，算出多个平均速度然后取平均值

B．减小挡光片上端到光电门的距离h

C．增大挡光片的挡光宽度b

D．适当减小挡光片的挡光宽度b

(4)若采用本装置测量当地的重力加速度g，则测量值________真实值（选填“大于”、“等于”或“小于”）．

【题目】光滑的长轨道形状如图所示，下部为半圆形，半径为 R=0.3 m，固定在竖直平面内。质量分别为 m、2m的两小环 A、B 用长为的轻杆连接在一起，套在轨道上，A 环距轨道底部高为，现将 A、B 两环从图示位置由静止释放。重力加速度为g，已知 sin 37°=0.6，cos 37°=0.8，求：

(1)运动过程中 A 环距轨道底部的最大高度；

(2)A环到达轨道底部时，A、B两环速度大小。

【题目】如图所示，站在车上的人，用锤子连续敲打小车。初始时，人、车、锤都静止。假设水平地面光滑，关于这一物理过程，下列说法正确的是

A. 连续敲打可使小车持续向右运动

B. 人、车和锤组成的系统机械能守恒

C. 当锤子速度方向竖直向下时，人和车水平方向的总动量为零

D. 人、车和锤组成的系统动量守恒

【题目】如图所示，半径为R,内径很小的光滑半圆管竖直放置，整个装置处在方向竖直向上的匀强电场中，两个质量均为m、带电量相同的带正电小球a、b,以不同的速度进入管内（小球的直径略小于半圆管的内经，且忽略两小球之间的相互作用），a通过最高点A时,对外管壁的压力大小为3、5mg，b通过最高点A时,对内管壁的压力大小0、25mg，已知两小球所受电场力的大小为重力的一半。

求（1）a、b两球落地点距A点水平距离之比；

（2）a、b两球落地时的动能之比。

【答案】（1）4∶3 （2）8∶3

【解析】

试题分析：（1）以a球为研究对象，设其到达最高点时的速度为，根据向心力公式有：

其中

解得：

以b球为研究对象，设其到达最高点时的速度为vb，根据向心力公式有：

其中

解得：

两小球脱离半圆管后均做平抛运动，根据可得它们的水平位移之比：

（2）两小球做类平抛运动过程中，重力做正功，电场力做负功，根据动能定理有：

对a球：

解得：

对b球：

解得：

则两球落地时的动能之比为：

考点：本题考查静电场、圆周运动和平抛运动，意在考查考生的分析综合能力。

【名师点睛】本题关键是对小球在最高点进行受力分析，然后根据向心力公式和牛顿第二定律求出平抛的初速度，再结合平抛运动规律求解。

【题型】解答题
【结束】
19

【题目】如图所示，倾角θ=37°的光滑且足够长的斜面固定在水平面上，在斜面顶端固定一个轮半径和质量不计的光滑定滑轮D，质量均为m=1kg的物体A和B用一劲度系数k=240N/m的轻弹簧连接，物体B被位于斜面底端且垂直于斜面的挡板P挡住。用一不可伸长的轻绳使物体A跨过定滑轮与质量为M的小环C连接，小环C穿过竖直固定的光滑均匀细杆，当整个系统静止时，环C位于Q处，绳与细杆的夹角α=53°，且物体B对挡板P的压力恰好为零。图中SD水平且长度 为d=0．2m，位置R与位置Q关于位置S对称，轻弹簧和定滑轮右侧的绳均与斜面平行。现 让环C从位置R由静止释放，sin37°=0．6，cos37°=0．8，g取10m/s2。

求：（1）小环C的质量 M；

（2）小环C通过位置S时的动能 Ek及环从位置R运动到位置S的过程中轻绳对环做的功WT；

（3）小环C运动到位置Q的速率v．

【题目】现代质谱仪可用来分析比质子重很多的离子，其示意图如图所示，其中加速电压恒定。质子在入口处从静止开始被加速电场加速，经匀强磁场偏转后从出口离开磁场。若某种一价正离子（质量为质子的121倍）在入口处从静止开始被同一加速电场加速，为使它经匀强磁场偏转后仍从同一出口离开磁场，需将磁感应强度增加到原来的

A.121倍B.14641倍

C.11倍D.12倍

【题目】如图所示，摩托车做腾跃特技表演，沿曲面冲上高0.8 m顶部水平高台，接着以v＝3m/s水平速度离开平台，落至地面时，恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道，并沿轨道下滑。A、B为圆弧两端点，其连线水平。已知圆弧半径R＝1.0m，人和车的总质量为180 kg，特技表演的全过程中，阻力忽略不计。g＝10 m/s2，sin53°＝0.8，cos53°＝0.6。求：（人和车可视为质点）

(1)从平台飞出到A点，人和车运动的水平距离s；

(2)从平台飞出到达A点时的速度及圆弧对应圆心角θ；

(3)人和车运动到达圆弧轨道A点时对轨道的压力。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网