题目内容
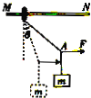
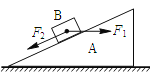
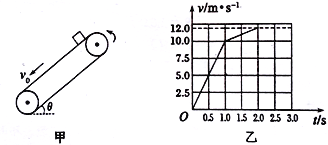
【题目】如图甲所示,倾角为的传送带以恒定的速率v0沿逆时针方向运行。t=0时,将质量m=1kg的炭块(可视为质点)轻放在传送带上,炭块相对地面的v-t图象如图乙所示,整个过程炭块未滑离传送带。设沿传送带向下为正方向,取重力加速度g=10m/s2。则
A. 传送带两轮间的距离为20m
B. 0~2.0s内摩擦力对炭块做功-24J
C. 0~2.0s内炭块与传送带摩擦产生的热量为24J
D. 炭块在传送带上的痕迹长度为4m
【答案】BC
【解析】
由图象可以得出物体先做匀加速直线运动,当速度达到传送带速度后,由于重力沿斜面向下的分力大于摩擦力,物块继续向下做匀加速直线运动,根据牛顿第二定律,结合加速度的大小求出动摩擦因数和倾角的大小,分别求出物体两次匀加速直线运动的位移,结合摩擦力的大小求出摩擦力对物体做功的大小;分别求出两个阶段的相对位移,根据Q=f△x,即可求出产生的热量;划痕即相对位移的长度,但第二阶段的划痕与第一阶段重合。
A. 由图象可以得出炭块先做匀加速直线运动,当速度达到传送带速度后,继续向下做匀加速直线运动,整个过程炭块未滑离传送带,所以传送带两轮间的距离应足够长,故A错误;
B.由图象可知,在01s内物块受到的摩擦力沿斜面向下,a1=(mgsinθ+μmgcosθ)/m=10m/s2;在12s内受到的摩擦力沿斜面向上,a2=mgsinθμmgcosθm=2m/s2;
联立两式解得:μ=0.5,θ=37.
第一段匀加速直线运动的位移为:x1=![]() ,
,
摩擦力做功为:Wf1=μmgcosθx1=0.5×10×0.8×5J=20J,
第二段匀加速直线运动的位移为:x2=![]() =11m,
=11m,
摩擦力做功为:Wf2=μmgcosθx2=0.5×10×0.8×11J=44J,
所以有:Wf=Wf1+Wf2=2044=24J.故B正确;
C. 第一段匀加速直线运动炭块和传送带间的相对位移为:△x1=v0t1-x1=10×1-5=5m,
产生的热量为:Q1=μmgcosθ△x1=0.5×10×0.8×5J=20J;
第二段匀加速直线运动炭块和传送带间的相对位移为:△x2=x2-v0t2=11-10×1=1m,
产生的热量为:Q2=μmgcosθ△x2=0.5×10×0.8×1J=4J;
0~2.0s内炭块与传送带摩擦产生的热量为Q=Q1+Q2=20J+4J=24J,故C正确;
D. 第一段匀加速直线运动传送带比炭块的位移大,划痕即炭块和传送带间的相对位移为5m;第二段匀加速直线运动炭块比传送带位移大,划痕即炭块和传送带间的相对位移为1m,所以总的划痕长度即第一阶段的划痕5m,故D错误。
故选:BC

 名校课堂系列答案
名校课堂系列答案【题目】某同学通过实验探究小灯泡的伏安特性曲线。除了导线、开关和小灯泡之外,实验室提供的器材还有:
A.电流表(A1):量程0—0.6A,内阻约0.125Ω
B.电流表(A2):量程0—3A,内阻约0.025Ω
C.电压表(V1):量程0—3V,内阻约3kΩ
D.电压表(V2):量程0—15V,内阻约15kΩ
E.滑动变阻器(R1):总阻值约10Ω
F.滑动变阻器(R2):总阻值约200Ω
G.一组干电池,其电动势为3.0V,内阻很小
该同学选择仪器,设计电路并进行实验,通过实验得到如下数据:
U/V | 0 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 |
I/A | 0 | 0.12 | 0.21 | 0.29 | 0.34 | 0.38 | 0.42 | 0.45 | 0.47 | 0.49 | 0.50 |


(1)请把该同学设计的实验电路图画在图甲的方框中___________________。
(2)在探究实验中该同学选择的器材是:电流表为_________,电压表为_________,滑动变阻器为___________(以上均填写器材代号)。
(3)请在图乙的坐标系中画出小灯泡的I—U图线________________。
(4)根据该实验的测量数据,得出的有关小灯泡电阻的结论是__________________;你对该实验结论的解释是________________________。
(5)用导线将该小灯泡直接连在某一电源的两极之间,要使小灯泡的实际发热功率约为0.27W。那么,电源的电动势和内电阻应该分别最接近_________________
A.1.5V、2.0Ω B.1.5V、0.5Ω
C.3.0V、0.5Ω D.3.0V、2.0Ω