题目内容
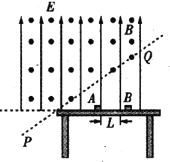
【题目】如图所示，半径为R的光滑半圆形轨道竖直固定且与水平地面相切于A点，在其右侧一定水平距离处固定一个倾角为
的斜面体，斜面体的顶端C离地面高度为h（2R＞h），底端E固定一轻质弹簧，原长为DE，斜面CD段粗糙而DE段光滑.现给一质量为m的小物块（可看作质点）一个水平初速度，从A处进入圆轨道到达最高点B，离开最高点B后恰能落到斜面体顶端C处，且速度方向恰好平行于斜面，小物块沿斜面下滑压缩弹簧后又沿斜面向上返回，第一次恰能返回到最高点C。小物块与斜面CD段的动摩擦因数为
，重力加速度为g，不计小物块碰撞弹簧时的机械能损失。求：
（1）小物块运动到B点时，对轨道的压力；
（2）弹簧的原长DE。
【答案】（1）
，方向竖直向上；（2）
【解析】
（1）小球B到C做平抛运动
=2g（2R-h）
在C点时
在B点，由牛顿第二定律得
F+mg=
由以上各式解得
由牛顿第三定律，物块在B点对轨道的压力为，方向竖直向上
（2）在C点，速度
从C点又返回C点，由动能定理
由几何知识得
CE=
弹簧的原长DE=CE-LCD
由以上各式解得
练习册系列答案
相关题目
