题目内容
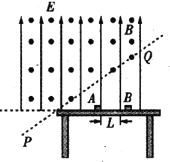
【题目】如图,在水平桌面上方区域内,存在竖直向上、电场强度E=![]() 的匀强电场,在过桌面左边缘的虚线PQ上方存在垂直纸面向外、磁感应强度B=
的匀强电场,在过桌面左边缘的虚线PQ上方存在垂直纸面向外、磁感应强度B=![]() T的匀强磁场,虚线PQ与水平桌面成45°角.现将一个质量m1=2.0×10-3kg、带正电q=+4.0×10-3C的小物块A静置在桌面上,质量m2=1.0×10-3kg、不带电的绝缘小物块B,从与A相距L=2.0m处的桌面上,以v0=5.0m/s的初速度向左运动,物块A、B与桌面间的动摩擦因数均为
T的匀强磁场,虚线PQ与水平桌面成45°角.现将一个质量m1=2.0×10-3kg、带正电q=+4.0×10-3C的小物块A静置在桌面上,质量m2=1.0×10-3kg、不带电的绝缘小物块B,从与A相距L=2.0m处的桌面上,以v0=5.0m/s的初速度向左运动,物块A、B与桌面间的动摩擦因数均为![]() =0.4,二者在桌面上发生弹性碰撞(碰撞时间极短),碰撞后B反弹的速vB=1.0m/s,A向左运动进入磁场,g取10m/s2。求:
=0.4,二者在桌面上发生弹性碰撞(碰撞时间极短),碰撞后B反弹的速vB=1.0m/s,A向左运动进入磁场,g取10m/s2。求:
(1)碰撞后A的速度;
(2)A从进入磁场到再次回到桌面上所用的时间;
(3)若经过一段时间后A、B在桌面上相遇,那么,碰撞前A与桌面左边缘的距离。
【答案】(1)![]() ,方向水平向左;(2)
,方向水平向左;(2)![]() ;(3)0.51m
;(3)0.51m
【解析】
(1)设B与A碰前瞬间的速度为v,碰后A的速度分别为vA、vB,对B由动能定理
![]()
A与B碰撞过程,对A、B组成的系统,由动量守恒定律
![]()
由以上各式解得
![]()
方向水平向左
(2)对A受力由于
![]()
碰后A向左做匀速直线运动,进入磁场做匀速圆周运动周期
![]()
由几何知识,A在磁场中运动了![]() 周期
周期
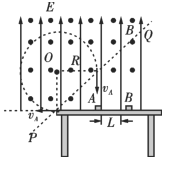
在磁场中时间
![]()
在磁场中
![]()
在磁场中半径
![]()
出磁场后运动时间
![]()
A从进入磁场到再次回到桌面上所用的时间
![]()
由以上各式解得
![]()
(3)碰后B反弹,在桌面上向右作匀减速运动,速度减少为零的时间为t3,根据牛顿第二定律
![]()
速度
![]()
解得
![]()
碰撞后B运动时间小于A运动时间,由此可知A、B相遇时,B已经停止运动,所以A、B相遇的位置为B停止运动的位置,也是A竖直向下再次回到桌面的位置
B向右匀减速的位移
![]()
A距桌边P的距离
![]()
由以上各式解得
![]()

练习册系列答案
相关题目