题目内容
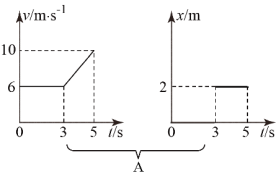
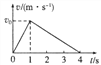
【题目】雪崩是自然灾害之一,我们在登雪山和欣赏雪山的美景时,一定要注意安全。某摄影爱好者站在倾角为37°的斜坡底端正在对斜坡顶端的美景进行拍摄,t0=0时,在距坡底为L=45m处发生雪崩,摄影受好者发现后经过t1=1s的反应时间,从静止开始以![]() 的加速度逃离。当摄影者的速度达到6m/s后就不能再加速了,并以此速度做匀速运动,如图所示。已知雪块(可视为质点)与坡面和地面间的动摩擦因数均为0.3,sin37°=0.6,cos37°=0.8,取g=10m/s2,假设雪块从坡面滑向水平面时速度大小不变。
的加速度逃离。当摄影者的速度达到6m/s后就不能再加速了,并以此速度做匀速运动,如图所示。已知雪块(可视为质点)与坡面和地面间的动摩擦因数均为0.3,sin37°=0.6,cos37°=0.8,取g=10m/s2,假设雪块从坡面滑向水平面时速度大小不变。
(1)求雪块到达斜面底端时的速度大小和下滑的时间;
(2)摄影者站在距坡底至少多远处才能安全逃离。
【答案】(1)18m/s,5s;(2)12m
【解析】
(1)当雪块在斜坡上运动时,根据受力情况由牛顿第二定律可知
![]()
代入数据解得
a=3.6m/s2
设雪块到达斜面底端时的速度为v,下滑过程中根据速度与位移的关系有![]()
代入数据解得
v=18m/s
根据速度与时间的关系有
![]()
代入数据解得
t=5s
(2)人加速到最大速度需要的时间为
![]()
又由于人的反应时间为1s,故当雪块到达斜面底端时,人恰好达到最大速度,所以人的位移为
![]()
此后雪块在水平面做减速运动,设雪块质量为m,则加速度大小为
![]()
人做匀速直线运动,设人开始站在离坡底的距离为x,则要使人安全逃离当雪块与人的速度相等时恰好追上人x最小,故对雪块有
![]() ,
,![]()
对人有
![]()
它们位移关系有
![]()
联立以上各式代入数据解得
x=12m
即摄影者站在距坡底至少12m远处才能安全逃离。

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目