题目内容
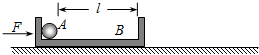
如图所示,光滑斜面、光滑水平面Ⅰ、光滑水平面Ⅱ及紧靠水平面Ⅰ的长木板M,木板上表面与水平面Ⅰ齐平,动摩擦μ=0.4.物块m1从高为h=7.2m处由静止释放无机械能损失滑到水平面Ⅰ,与m2碰后立即粘为一体,两物块滑到木板右端时恰好与木板相对静止.已知:m1=m2=1kg,M═4kg,g=10m/s2.求:
①物块m1与物块m2碰后,两物块的速度大小;
②木板的长度L.

①物块m1与物块m2碰后,两物块的速度大小;
②木板的长度L.

①(1)设物块m1由静止滑到光滑水平面Ⅰ上时的速度为v1,由机械能守恒得:
m1gh=
m1v12,
代入数据解得:v1=12m/s,
以两物块组成的系统为研究对象,两物块碰撞过程动量守候,以向右为正方向,由动量守候定律得:
m1v1=(m1+m2)v2,
代入数据解得:v2=6m/s;
②两物块滑上木板后,以物块与木板组成的系统为研究对象,以向右为正方向,由动量守恒定律得:
(m1+m2)v2=(m1+m2+M)v3,
代入数据得:v3=2m/s,
由能量守恒定律得:μ(m1+m2)gL=
(m1+m2)v22-
(m1+m2+M)v32,
代入数据解得:L=3m;
答:①物块m1与物块m2碰后,两物块的速度大小为6m/s;
②木板的长度为3m.
m1gh=
| 1 |
| 2 |
代入数据解得:v1=12m/s,
以两物块组成的系统为研究对象,两物块碰撞过程动量守候,以向右为正方向,由动量守候定律得:
m1v1=(m1+m2)v2,
代入数据解得:v2=6m/s;
②两物块滑上木板后,以物块与木板组成的系统为研究对象,以向右为正方向,由动量守恒定律得:
(m1+m2)v2=(m1+m2+M)v3,
代入数据得:v3=2m/s,
由能量守恒定律得:μ(m1+m2)gL=
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:L=3m;
答:①物块m1与物块m2碰后,两物块的速度大小为6m/s;
②木板的长度为3m.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目