Question

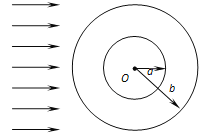
【题目】两个天体(包括人造天体)间存在万有引力，并具有由相对位置决定的势能.如果两个天体的质量分别为m1和m2，当它们相距无穷远时势能为零，则它们的距离为r时，引力势能Ep=-G.发射地球同步卫星时，一般是把它先送入较低的圆形轨道，如图所示，再经过两次点火，即先在图中a点处启动燃气发动机，向后喷出高压燃气，卫星得到加速，进入图中的椭圆轨道Ⅱ；在轨道Ⅱ的远地点b处第二次点火，卫星再次被加速，此后，卫星沿图中的圆形轨道Ⅲ(同步轨道)运动.设某同步卫星的质量为m，地球半径为R，轨道Ⅰ距地面非常近，轨道Ⅲ距地面的距离近似为6R，地面处的重力加速度为g，并且每次点火经历的时间都很短，点火过程中卫星减少的质量可以忽略.

（1）从轨道Ⅰ转移到轨道Ⅲ的过程中，合力对卫星所做的总功是多大？

（2）若已知卫星在轨道Ⅱ上经过a点时的速率为，则在b处点火的过程中燃气对卫星所做的功是多少？

Answer 1

【答案】(1) (2)

【解析】（1）卫星在轨道Ⅰ和轨道Ⅲ做圆周运动，应满足：

，

得：

合力做的功：

（2）卫星在a处的势能：

卫星在b处的势能：

卫星在轨道Ⅱ上经过b处的速度为υb，由机械能守恒定律有：

,

解得：

故在a处燃气所做的功: .