题目内容
12. A、B两个小球半径相同,质量不同,并排悬挂在同样长度的绳子上,彼此相互接触,把质量为m0的A球拉开后由静止释放,当A球与B球相碰前其速度为v0,碰撞后量小球的动量相等,则:
A、B两个小球半径相同,质量不同,并排悬挂在同样长度的绳子上,彼此相互接触,把质量为m0的A球拉开后由静止释放,当A球与B球相碰前其速度为v0,碰撞后量小球的动量相等,则:①求碰撞后A球的速度
②若碰撞我弹性碰撞,求碰撞后B球的动能.
分析 ①两球碰撞过程系统动量守恒,应用动量守恒定律可以求出碰撞后A的速度;
②应用动量守恒定律与机械能守恒定律可以求出碰撞后B的动能.
解答 解:①两球碰撞过程系统动量守恒,以碰撞前A的速度方向为正方向,由动量守恒定律得:
m0v0=pA+pB,
由题意可知,碰撞后两球的动量相等,即:pA=pB,
解得:pA=$\frac{1}{2}$m0v0=m0v,
碰撞后A的速度:v=$\frac{1}{2}$v0;
②碰撞为弹性碰撞,碰撞过程机械能守恒,由机械能守恒定律得:
$\frac{1}{2}$m0v02=$\frac{1}{2}$m0v2+EKB,
解得:EKB=$\frac{3}{8}$m0v02;
答:①求碰撞后A球的速度为$\frac{1}{2}$v0;
②若碰撞我弹性碰撞,求碰撞后B球的动能为$\frac{3}{8}$m0v02.
点评 本题考查了求球的速度与动能,两球发生弹性碰撞,碰撞过程动量守恒、机械能守恒,分析清楚球的运动过程,应用动量守恒定律与机械能守恒定律可以解题.

练习册系列答案
相关题目
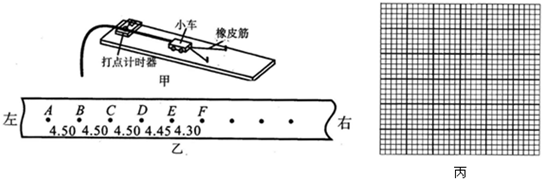
2.某实验小组采用如图甲所示的装置探究功与速度变化的关系.
(1)在一次实验中得到了一条如图乙所示的纸带,图中数据为相邻两点的距离,下列说法正确的是BDE
A.纸带的左端是与小车相连的
B.纸带的右端是与小车相连的
C.利用C、D、E、F这些点之间的距离来确定小车的速度
D.利用A、B、C、D这些点之间的距离来确定小车的速度
E.实验中木板略微倾斜,这样做的目的是可使得橡皮筋做的功等于合外力对小车做的功
(2)下面是本实验的数据记录表:
为进一步直观反映功与速度变化的关系,请根据如表数据,选择恰当的物理量在图丙所示的坐标系中作出相应的图象.
由图象得出的结论在误差范围允许内,橡皮筋对小车做的功等于小车动能的改变量.
(1)在一次实验中得到了一条如图乙所示的纸带,图中数据为相邻两点的距离,下列说法正确的是BDE
A.纸带的左端是与小车相连的
B.纸带的右端是与小车相连的
C.利用C、D、E、F这些点之间的距离来确定小车的速度
D.利用A、B、C、D这些点之间的距离来确定小车的速度
E.实验中木板略微倾斜,这样做的目的是可使得橡皮筋做的功等于合外力对小车做的功
(2)下面是本实验的数据记录表:
| 数据 项目 次数 | 橡皮筋做的功 | 10个均匀间隔的距离xn(m) | 10个间隔的时间t(s) | 小车获得的速度vn(m/s) | 小车速度的平方vn2(m2/s2) |
| 1 | W | 0.288 | 0.2 | 1.44 | 2.07 |
| 2 | 2W | 0.417 | 0.2 | 2.09 | 4.37 |
| 3 | 3W | 0.489 | 0.2 | 2.45 | 6.00 |
| 4 | 4W | 0.590 | 0.2 | 2.95 | 8.70 |
| 5 | 5W | 0.648 | 0.2 | 3.24 | 10.50 |
由图象得出的结论在误差范围允许内,橡皮筋对小车做的功等于小车动能的改变量.

20.地球半径为R,地面重力加速度为g,地球自转周期为T,地球同步卫星离地面的高度为h,则地球同步卫星的线速度大小为( )
| A. | $\sqrt{(R+h)g}$ | B. | $\sqrt{\frac{{R}^{2}g}{R+h}}$ | C. | $\frac{2π(R+h)}{T}$ | D. | $\frac{2πR}{T}$ |
17. 弹道导弹是指在火箭发动机推力作用下按预定轨道飞行,关闭发动机后按自由抛体轨迹飞行的导弹.若关闭发动机时导弹的速度是水平的,不计空气阻力,则导弹从此时起水平方向的位移( )
弹道导弹是指在火箭发动机推力作用下按预定轨道飞行,关闭发动机后按自由抛体轨迹飞行的导弹.若关闭发动机时导弹的速度是水平的,不计空气阻力,则导弹从此时起水平方向的位移( )
 弹道导弹是指在火箭发动机推力作用下按预定轨道飞行,关闭发动机后按自由抛体轨迹飞行的导弹.若关闭发动机时导弹的速度是水平的,不计空气阻力,则导弹从此时起水平方向的位移( )
弹道导弹是指在火箭发动机推力作用下按预定轨道飞行,关闭发动机后按自由抛体轨迹飞行的导弹.若关闭发动机时导弹的速度是水平的,不计空气阻力,则导弹从此时起水平方向的位移( )| A. | 只由水平速度决定 | B. | 只由离地高度决定 | ||
| C. | 由水平速度、离地高度共同决定 | D. | 与水平速度、离地高度都没有关系 |
1.物体受几个恒力作用做匀速直线运动,现撤去一个恒力,则物体接下来可能的运动是( )
| A. | 匀速直线运动 | B. | 匀变速直线运动 | C. | 匀速圆周运动 | D. | 匀变速曲线运动 |
2.下列说法正确的是( )
| A. | 导体中电荷运动就形成电流 | |
| B. | 电流的方向,它量一个矢量 | |
| C. | 在国际单位制中,电流的单位是安培 | |
| D. | 任何物体,只要其两端电势差不为零,就有电流存在 |
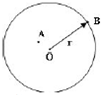 如图所示为圆心为O,半径为r的圆盘,圆盘绕垂直于过O点的轴匀速转动,转动角速度为ω,A、B为圆盘上的两点,OA长为$\frac{r}{3}$,OB长为r,则A点的线速度大小为$\frac{ωr}{3}$,B点的加速度大小为ω2r.
如图所示为圆心为O,半径为r的圆盘,圆盘绕垂直于过O点的轴匀速转动,转动角速度为ω,A、B为圆盘上的两点,OA长为$\frac{r}{3}$,OB长为r,则A点的线速度大小为$\frac{ωr}{3}$,B点的加速度大小为ω2r. 如图所示,倾角为θ的直角斜面体固定在水平地面上,其顶端固定有一轻质定滑轮,轻质弹簧和轻质细绳相连,一端接质量为m2的物块B,物块B放在地面上且使滑轮和物块间的细绳竖直,一端连接质量为m1的物块A,物块A放在光滑斜面上的P点保持静止,弹簧和斜面平行,此时弹簧具有的弹性势能为Ep.不计定滑轮、细绳、弹簧的质量,不计斜面、滑轮的摩擦,已知弹簧劲度系数为k,P点到斜面底端的距离为L.现将物块A缓慢斜向上移动,直到弹簧刚恢复原长时的位置,并由静止释放物块A,当物块B刚要离开地面时,物块A的速度即变为零,求:在以后的运动过程中物块A最大速度的大小.
如图所示,倾角为θ的直角斜面体固定在水平地面上,其顶端固定有一轻质定滑轮,轻质弹簧和轻质细绳相连,一端接质量为m2的物块B,物块B放在地面上且使滑轮和物块间的细绳竖直,一端连接质量为m1的物块A,物块A放在光滑斜面上的P点保持静止,弹簧和斜面平行,此时弹簧具有的弹性势能为Ep.不计定滑轮、细绳、弹簧的质量,不计斜面、滑轮的摩擦,已知弹簧劲度系数为k,P点到斜面底端的距离为L.现将物块A缓慢斜向上移动,直到弹簧刚恢复原长时的位置,并由静止释放物块A,当物块B刚要离开地面时,物块A的速度即变为零,求:在以后的运动过程中物块A最大速度的大小.