题目内容
【题目】(20分)如图，中空的水平圆形转盘内径r=0.6m，外径足够大，沿转盘某条直径有两条光滑凹槽，凹槽内有A、B、D、E四个物块，D、E两物块分别被锁定在距离竖直转轴R=1.0m处，A、B紧靠D、E放置两根不可伸长的轻绳，每根绳长L=1.4m，一端系在C物块上，另一端分别绕过转盘内侧的光滑小滑轮，穿过D、E两物块中间的光滑圆孔，系在A、B两个物块上，A、B、D、E四个物块的质量均为m=0.1㎏，C物块的质量
=2.0kg，所有物块均可视为质点，(取重力加速度g=10m/s)，计算结果可用最简的分式与根号表示）
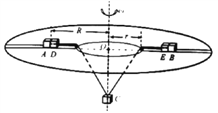
(1)启动转盘，转速缓慢增大，求A、D以及B、E之间恰好无压力时的细绳的拉力及转盘的角速度；
(2)停下转盘后，将C物块置于圆心O处，并将A、B向外测移动使轻绳水平拉直，然后无初速度释放A、B、C物块构成的系统，求A、D以及B、E相碰前瞬间C物块的速度；
(3)碰前瞬间解除对D、E物块的锁定，若A、D以及B、E一经碰撞就会粘在一起，且碰撞时间极短，求碰后C物块的速度.
【答案】(1) 
(2) 
(3) 
【解析】试题分析：AB在细绳拉力作用下做，做匀速圆周运动。C在拉力作用下处于平衡态，结合轻绳上的拉力大小相等可求细绳的拉力及转盘的角速度；轻绳水平拉直，然后无初速度释放，A、B、C物块构成的系统机械能守恒，结合关联速度的知识，可求C物块的速度；碰前瞬间解除对D、E物块的锁定，由动量定理可求C物块的速度。
（1）C物块保持静止故
， 
， 
对A、B两个物块
角速度
（2）设碰前A、B速度大小为
，C的速度大小为
，
由绳长不变可知： 
系统下落过程中机械能守恒： 
由几何关系h=0.8m
得： 
（3）设碰后A、D的速度大小为
，C的速度大小为
由绳长不变
设绳上拉力的冲量大小为I，由于碰撞时间极短，绳子拉力远大于重力。
对C物块运用动量定理： 
对A、D运用动量定理： 
得： 
