Question

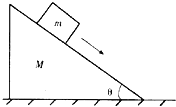
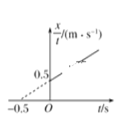
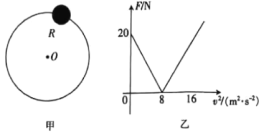
【题目】如图甲所示，小球（视为质点）穿在竖直平面内光滑的固定圆环上，绕圆心O点做半径 为R的圆周运动。小球运动到最髙点时，圆环对小球的弹力大小为F，小球在最高点的速度 大小为v，其F—v2图象如图乙所示。取重力加速度大小g=10 m/s2，不计空气阻力。求：

（1）小球的质量和圆环的半径；

（2）小球在最高点受到向上的弹力大小为15N时的速度大小。（结果可保留根式）

Answer 1

【答案】（1）0. 8m。（2）m/s。

【解析】

由题中“小球（视为质点）穿在竖直平面内光滑的固定圆环上”可知，本题考查圆周运动向心力的问题，根据向心力公式可解答本题。

（1）由图可知，当速度为零时，小球所受的弹力等于小球的重力，因此可得小球的质量为

当时，小球恰好不受弹力，故其重力提供向心力，因此可得

解得

（2）小球在最高点受到向上的弹力大小为15N时，小球所受合力为5N，方向指向圆心，可得

解得