Question

【题目】如图所示，在场强E＝104 N/C的水平匀强电场中，有一根长l＝15 cm的细线，一端固定在O点，另一端系一个质量m＝3 g、电荷量q＝2×10－6 C的带正电小球，当细线处于水平位置时，小球从静止开始释放，g取10 m/s2.求：

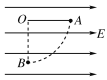
(1)若取A点电势为零，小球在B点的电势能、电势分别为多大？

(2)小球到B点时速度为多大？绳子张力为多大？

Answer 1

【答案】(1)3×10－3J，1.5×103 V；(2)1m/s，5×10－2N

【解析】

（1）从A到B电势能的变化量为：△Ep电=Eql=3×10-3J
若取A点电势为零，小球在B点的电势能：Ep=△Ep电=3×10-3J
由Ep=φBq得： φB=V=1.5×103V
（2）A→B由动能定理得： mgl-Eql=mvB2
代入解得：vB=1m/s
在B点，对小球由牛顿第二定律得：FT-mg=m
得：FT=5×10-2N