题目内容
(14分)如图所示,固定在水平桌面上的光滑金属导轨MN、PQ,间距为L,其右端接有阻值为R的电阻和理想交流电压表,整个装置处在竖直向下的匀强磁场中,磁感应强度大小为B.导体棒ef垂直于导轨放置,且与两导轨接触良好,导体棒接入电路的电阻为r,其它电阻不计,现让导体棒在ab、cd之间往复运动,其速度随时间的关系为 (vm和T已知).
(vm和T已知).
(1)写出导体棒产生的电动势的表达式,并求出电压表的示数;
(2)求一个周期T内R中产生的焦耳热Q;
(3)若ab与cd的距离为x,求导体棒从ab滑到cd过程中通过电阻R的电量q.
⑴e=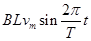 ,UR=
,UR=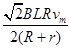 ;⑵Q=
;⑵Q=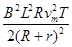 ;⑶q=
;⑶q=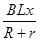 。
。
解析试题分析:⑴根据法拉第电磁感应定律可知导体棒由于切割磁感线而产生的感应电动势为:e=BLv ①
又因为v=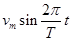 ②
②
根据闭合电路欧姆定律可知,电阻R两端的电压瞬时值为:u=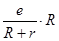 ③
③
由①②③式联立解得:e=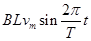 ,u=
,u=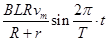
显然R两端的电压瞬时值随时间t成正弦函数关系变化,又根据电路分析可知,电压表测出的是电阻R两端电压的有效值,因此其读数为:UR=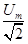 =
=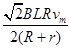 ④
④
根据焦耳定律可知,在一个周期T内R中产生的焦耳热为:Q=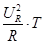 ⑤
⑤
由④⑤式联立解得: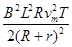
⑶根据电流的定义式可知,在导体棒从ab滑到cd过程中通过电阻R的电量为:q=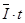 ⑥
⑥
根据闭合电路欧姆定律有: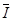 =
=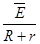 ⑦
⑦
根据法拉第电磁感应定律可知: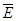 =
=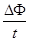 ⑧
⑧
在导体棒从ab滑到cd过程中,回路中的磁通变化量为:ΔΦ=BΔS=BLx ⑨
由⑥⑦⑧⑨式联立解得:q=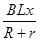
考点:本题主要考查法拉第电磁感应定律、焦耳定律的应用及交变电流的四值运算问题,属于中档题。

某小型发电机产生的交变电动势为e=50sin100πt(V),对此电动势,下列表述正确的有 ( )
A.最大值是50 V V | B.频率是100Hz |
C.有效值是25 V V | D.周期是0.02s |
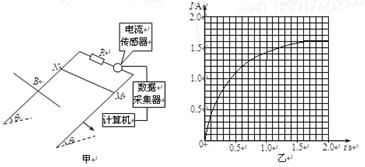
如图甲所示,理想变压器原、副线圈的匝数比为3∶1,L1、L2、L3为三只规格均为“9V 6W”的相同灯泡,各电表均为理想交流电表,输入端接入如图乙所示的交变电压,则以下说法中正确的是:( )
| A.电流表的示数为2A |
B.电压表的示数为 V V |
| C.副线圈两端接入耐压值为9V的电容器能正常工作 |
| D.变压器副线圈中交变电流的频率为50Hz |
 x(m),磁感应强度大小B=2 T.线框在沿x轴正方向的拉力F作用下,以速度v=1 m/s水平向右做匀速直线运动,直到拉出磁场.
x(m),磁感应强度大小B=2 T.线框在沿x轴正方向的拉力F作用下,以速度v=1 m/s水平向右做匀速直线运动,直到拉出磁场.


