题目内容
两根足够长的光滑平行直导轨MN、PQ与水平面成θ角放置,两导轨间距为L,M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直于导轨平面向上,导轨和金属杆接触良好,它们的电阻不计.现让ab杆由静止开始沿导轨下滑.
(1)求ab杆下滑的最大速度vm;
(2)ab杆由静止释放至达到最大速度的过程中,电阻R产生的焦耳热为Q,求该过程中ab杆下滑的距离x及通过电阻R的电量q.
(1) (2)
(2)  , q=
, q=
解析试题分析:(1)金属杆ab切割磁感线产生的感应电动势大小为E="BLv"
电路中电流
金属杆所受安培力FA=BIL
设金属杆ab运动的加速度为a,则
Mgsinθ - FA=ma
当加速度 为零时,速度
为零时,速度 达最大,速度最大值为
达最大,速度最大值为
(2)根据能量守恒定律有
解得
根据法拉第电磁感应定律有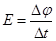
根据闭合电路欧姆定律 有
故感应电荷量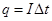
解得q=
考点:此题考查了法拉第电磁感应定律、牛顿第二定律及能量守恒定律。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
如图所示,LC振荡电路的导线及自感线圈的电阻忽略不计,某瞬间回路中电流方向如箭头所示,且此时电容器的极板A带正电荷,则该瞬间:
| A.电流i正在增大,线圈L中的磁场能也正在增大 |
| B.电容器两极板间电压正在增大 |
| C.电容器带电量正在减小 |
| D.线圈中电流产生的磁场的磁感应强度正在增强 |
一矩形线圈在匀强磁场中匀速转动,产生的交变电流电动势 (V),则( )
(V),则( )
A.交流电的电动势峰值是 V V |
| B.交流电的电动势有效值是220V |
| C.当t=0时,线圈平面恰好与中性面重合 |
D.当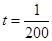 s时,e值为110V s时,e值为110V |
图甲所示的变压器原、副线圈匝数比为3:1,图乙是该变压器cd输入端交变电压u的图像,L1、L2、L3、L4为四只规格均为“9 V,6 W”的相同灯泡,各电表均为理想交流电表, 下说法正确的是
A.ab输入端电压的瞬时值表达式为 (V) (V) |
| B.电流表的示数为2A,且四只灯泡均能正常发光 |
| C.流过灯L2的电流每秒钟方向改变50次 |
| D.ab输人端输入功率Pab="18" W |

 的初速度沿框架向左运动,棒与框架的动摩擦因数为
的初速度沿框架向左运动,棒与框架的动摩擦因数为 ,测得棒在整个运动过程中,通过任一截面的电量为q,求:(1)棒能运动的距离?(2)R上产生的热量?
,测得棒在整个运动过程中,通过任一截面的电量为q,求:(1)棒能运动的距离?(2)R上产生的热量?

 (vm和T已知).
(vm和T已知).
 =30°,匀强磁场方向垂直框架平面向上,且B=0.2T,导体棒ab的质量m=0.2kg,R=0.1
=30°,匀强磁场方向垂直框架平面向上,且B=0.2T,导体棒ab的质量m=0.2kg,R=0.1 ,水平跨在导轨上,且可无摩擦滑动(g取10m/s2)求:
,水平跨在导轨上,且可无摩擦滑动(g取10m/s2)求: