题目内容
19.试根据表中数据,归纳出球形物体所受的空气阻力f与球的速度v及球的半径r的关系式为( )| A. | f=10vr(N) | B. | f=10vr2(N) | C. | f=5vr(N) | D. | f=5vr2(N) |
分析 对表中数据分析发现:vr2 与m成正比,由收尾速度时 f=mg 得f与m、vr2 成正比即:f=kvr2,然后求出比例系统k,由归纳法得出结论
解答 解:对表中数据分析发现:
即:$\frac{{r}^{2}v}{m}=2$即 vr2 与m成正比
由收尾速度时 f=mg 得f与m、vr2 成正比
即:f=kvr2
求比例系数K:K=$\frac{mg}{{vr}^{2}}$
对A小球,K=$\frac{{m}_{A}g}{{{{v}_{A}r}_{A}}^{2}}$=$\frac{2×10}{16{×0.5}^{2}}=5$(Ns/m3),
对B小球,$\frac{{m}_{B}g}{{{{v}_{B}r}_{B}}^{2}}=\frac{5×10}{40{×0.5}^{2}}=5$(Ns/m3),
对C小球,$\frac{{m}_{C}g}{{{{v}_{C}r}_{C}}^{2}}=\frac{45×10}{40{×1.5}^{2}}=5$(Ns/m3),
由归纳法得:k=5(Ns/m3),所以 f=5vr2.
故选:D.
点评 本题考查收尾速度、小球半径以及阻力的关系,关键知道物体达到收尾速度时重力等于阻力,要学会应用控制变量法解题,还要学会分析数据.

练习册系列答案
相关题目
9.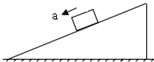 如图,粗糙的水平地面上有一质量为M的斜劈,斜劈上一质量为m的物块由静止沿斜面匀加速下滑,斜劈始终保持静止,则( )
如图,粗糙的水平地面上有一质量为M的斜劈,斜劈上一质量为m的物块由静止沿斜面匀加速下滑,斜劈始终保持静止,则( )
 如图,粗糙的水平地面上有一质量为M的斜劈,斜劈上一质量为m的物块由静止沿斜面匀加速下滑,斜劈始终保持静止,则( )
如图,粗糙的水平地面上有一质量为M的斜劈,斜劈上一质量为m的物块由静止沿斜面匀加速下滑,斜劈始终保持静止,则( )| A. | 地面对斜劈的摩擦力向右 | B. | 地面对斜劈的摩擦力向左 | ||
| C. | 斜劈对地面的压力大于(M+m)g | D. | 斜劈对地面的压力小于(M+m)g |
10.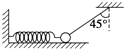 水平面上有一个质量为m=2kg的小球,小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连,如图所示,此时小球处于静止状态,且水平面对小球的弹力恰好为零.已知小球与水平面间的动摩擦因数μ=0.2,当剪断轻绳的瞬间,取g=10m/s2,以下说法正确的是( )
水平面上有一个质量为m=2kg的小球,小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连,如图所示,此时小球处于静止状态,且水平面对小球的弹力恰好为零.已知小球与水平面间的动摩擦因数μ=0.2,当剪断轻绳的瞬间,取g=10m/s2,以下说法正确的是( )
 水平面上有一个质量为m=2kg的小球,小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连,如图所示,此时小球处于静止状态,且水平面对小球的弹力恰好为零.已知小球与水平面间的动摩擦因数μ=0.2,当剪断轻绳的瞬间,取g=10m/s2,以下说法正确的是( )
水平面上有一个质量为m=2kg的小球,小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连,如图所示,此时小球处于静止状态,且水平面对小球的弹力恰好为零.已知小球与水平面间的动摩擦因数μ=0.2,当剪断轻绳的瞬间,取g=10m/s2,以下说法正确的是( )| A. | 此时轻弹簧的弹力大小为20N | |
| B. | 小球的加速度大小为8m/s2,方向向左 | |
| C. | 若剪断弹簧,则剪断的瞬间小球的加速度大小为10m/s2,方向向右 | |
| D. | 若剪断弹簧,则剪断的瞬间小球的加速度为0 |
7. 如图,在倾角为α的固定光滑斜面上,有一用绳子栓着的长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )
如图,在倾角为α的固定光滑斜面上,有一用绳子栓着的长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )
 如图,在倾角为α的固定光滑斜面上,有一用绳子栓着的长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )
如图,在倾角为α的固定光滑斜面上,有一用绳子栓着的长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )| A. | $\frac{g}{2}$sinα | B. | 1.5gsinα | C. | gsinα | D. | 2gsinα |
14.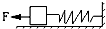 如图所示,物体重为100N,放在水平面上,物体右端与一轻弹簧连接,物体与地面的最大静摩擦力为40N,用一水平向左的30N的力作用于物体时,物体保持静止.则物体所受弹簧的弹力大小可能是( )
如图所示,物体重为100N,放在水平面上,物体右端与一轻弹簧连接,物体与地面的最大静摩擦力为40N,用一水平向左的30N的力作用于物体时,物体保持静止.则物体所受弹簧的弹力大小可能是( )
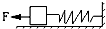 如图所示,物体重为100N,放在水平面上,物体右端与一轻弹簧连接,物体与地面的最大静摩擦力为40N,用一水平向左的30N的力作用于物体时,物体保持静止.则物体所受弹簧的弹力大小可能是( )
如图所示,物体重为100N,放在水平面上,物体右端与一轻弹簧连接,物体与地面的最大静摩擦力为40N,用一水平向左的30N的力作用于物体时,物体保持静止.则物体所受弹簧的弹力大小可能是( )| A. | 20N | B. | 40N | C. | 60N | D. | 80N |
11.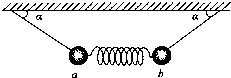 如图所示,轻弹簧两端拴接两个质量均为m的小球a、b,拴接小球的细线固定在天花板上,两球静止,两细线与水平方向的夹角均为α=30°,弹簧水平,以下说法正确的是( )
如图所示,轻弹簧两端拴接两个质量均为m的小球a、b,拴接小球的细线固定在天花板上,两球静止,两细线与水平方向的夹角均为α=30°,弹簧水平,以下说法正确的是( )
 如图所示,轻弹簧两端拴接两个质量均为m的小球a、b,拴接小球的细线固定在天花板上,两球静止,两细线与水平方向的夹角均为α=30°,弹簧水平,以下说法正确的是( )
如图所示,轻弹簧两端拴接两个质量均为m的小球a、b,拴接小球的细线固定在天花板上,两球静止,两细线与水平方向的夹角均为α=30°,弹簧水平,以下说法正确的是( )| A. | 细线的拉力大小为2mg | |
| B. | 弹簧的弹力大小为$\sqrt{3}$mg | |
| C. | 剪断左侧细线瞬间,b球加速度大小为$\frac{1}{2}$g | |
| D. | 剪断弹簧最左侧瞬间,a球加速度大小为0 |
9.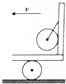 如图所示,一辆汽车的平直公路上向左行驶,一个质量为m、半径为R的球,用一轻绳悬挂在车厢竖直的光滑的后壁上.汽车以加速度a加速前进.绳子对球的拉力设为T,车厢后壁对球的水平弹力为N.则当汽车的加速度a增大时( )
如图所示,一辆汽车的平直公路上向左行驶,一个质量为m、半径为R的球,用一轻绳悬挂在车厢竖直的光滑的后壁上.汽车以加速度a加速前进.绳子对球的拉力设为T,车厢后壁对球的水平弹力为N.则当汽车的加速度a增大时( )
 如图所示,一辆汽车的平直公路上向左行驶,一个质量为m、半径为R的球,用一轻绳悬挂在车厢竖直的光滑的后壁上.汽车以加速度a加速前进.绳子对球的拉力设为T,车厢后壁对球的水平弹力为N.则当汽车的加速度a增大时( )
如图所示,一辆汽车的平直公路上向左行驶,一个质量为m、半径为R的球,用一轻绳悬挂在车厢竖直的光滑的后壁上.汽车以加速度a加速前进.绳子对球的拉力设为T,车厢后壁对球的水平弹力为N.则当汽车的加速度a增大时( )| A. | T不变,N增大 | B. | T增大,N增大 | C. | T减小,N减小 | D. | T减小,N变大 |
 如图所示,光滑固定的竖直杆上套有一个质量为m的小物块A,不可伸长的轻质细绳左端与物块A 相连,绕过固定在墙壁上、大小可忽略的定滑轮D后,右端作用恒定拉力F,虚线CD水平,间距为d,此时连接物块A的细绳与竖直杆的夹角为37°,物块A恰能保持静止.现瞬间调整绳右端的拉力为 F1=4F,使得物块从图示位置开始向上运动并通过C点,不计摩擦和空气阻力,重力加速度为g,cos37°=0.8,sin37°=0.6.求:
如图所示,光滑固定的竖直杆上套有一个质量为m的小物块A,不可伸长的轻质细绳左端与物块A 相连,绕过固定在墙壁上、大小可忽略的定滑轮D后,右端作用恒定拉力F,虚线CD水平,间距为d,此时连接物块A的细绳与竖直杆的夹角为37°,物块A恰能保持静止.现瞬间调整绳右端的拉力为 F1=4F,使得物块从图示位置开始向上运动并通过C点,不计摩擦和空气阻力,重力加速度为g,cos37°=0.8,sin37°=0.6.求: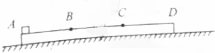 如图所示,长为3L的长木板AD放在光滑的水平面上,B、C两点将长木板三等分.AB,CD段光滑.一物块从A点以一定的初速度滑上长木板.物块与BC段间的动摩擦因数为μ,物块质量为m,长木板的质量为2m.重力加速度为g.
如图所示,长为3L的长木板AD放在光滑的水平面上,B、C两点将长木板三等分.AB,CD段光滑.一物块从A点以一定的初速度滑上长木板.物块与BC段间的动摩擦因数为μ,物块质量为m,长木板的质量为2m.重力加速度为g.