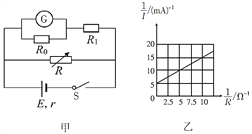
题目内容
【题目】如图所示,倾角θ=37°的斜面体固定在水平地面上,斜面长L=2.5m.质量M=2.0kg的B物体放在斜面底端,与斜面间的动摩擦因数μ=0.25,通过轻细绳跨过光滑的定滑轮与A物体相连接,连接B的细绳与斜面平行.A的质量m=2.5kg,绳拉直时用手托住A物体使其在距地面h高处由静止释放,着地后立即停止运动. A、B物体均可视为质点,取g=10m/s2,sin37=0.6,cos37=0.8.
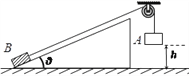
(1)求A物体下落的加速度大小及绳子拉力T的大小;
(2)求当A物体从多高处静止释放,B物体恰好运动至斜面最高点;
(3)若A物体从h=![]() m处静止释放,要使B物体向上运动且不从斜面顶端滑出,求A物体质量m的取值范围.(设B物体受到的最大静摩擦力等于滑动摩擦力)
m处静止释放,要使B物体向上运动且不从斜面顶端滑出,求A物体质量m的取值范围.(设B物体受到的最大静摩擦力等于滑动摩擦力)
【答案】(1)a=2 m/s2 T=20 N;(2)h=2 m;(3)![]()
【解析】(1)根据牛顿第二运动定律
根据牛顿第二定律对A有: ![]()
根据牛顿第二定律对B有: ![]()
代入数据解得: ![]()
绳子拉力大小: ![]()
(2)设物体A着地时B的速度为v,A着地后B做匀减速运动的加速度大小为a1
根据牛顿第二定律对B有: ![]()
代入数据解得: ![]()
对B由运动学公式得:
着地前: ![]()
着地后: ![]()
代入数据解得: ![]()
(3)设A着地后B向上滑行距离x
由运动学公式得: ![]()
位移关系满足: ![]()
着地前: ![]()
代入数据解得: ![]()
另一方面要能拉动必须有: ![]()
解得: ![]()
所以物体A的质量范围是: ![]()

【题目】如图所示,t=0时,质量为0.5kg的物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(经过B点前后速度大小不变),最后停在C点.每隔2s物体的瞬时速度记录在下表中,重力加速度g=10m/s2 , 则下列说法中正确的是( )
t/s | 0 | 2 | 4 | 6 |
v/(ms﹣1) | 0 | 8 | 12 | 8 |
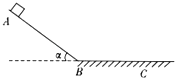
A.t=3s的时刻物体恰好经过B点
B.t=10s的时刻物体恰好停在C点
C.物体运动过程中的最大速度为12m/s
D.A,B间的距离小于B,C间的距离