��Ŀ����
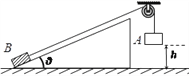
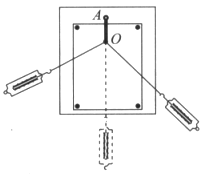
����Ŀ��ij�����ֱ�����ʾ��ͼ��ͼ��ʾ������Ϊm=0.1 kg��С���ڳ�ΪL�ĸ���(L�㹻��)���Ǽ�Ķ�Ħ������Ϊ![]() .�����뾶��ΪR=0.4m���ķ�֮һԲ���ƴ�Ӻ������B��ƽ������(���Ӵ����Ȳ���).����Բ��Բ��O1��O2�ȸߣ�Բ�������Ϊ�⻬��C��������ˮƽ������װ�ô���ͬһ��ֱƽ���ڣ���C��ˮƽ����Ϊd=0.8m�ĵ÷���MIN�������Ϊ
.�����뾶��ΪR=0.4m���ķ�֮һԲ���ƴ�Ӻ������B��ƽ������(���Ӵ����Ȳ���).����Բ��Բ��O1��O2�ȸߣ�Բ�������Ϊ�⻬��C��������ˮƽ������װ�ô���ͬһ��ֱƽ���ڣ���C��ˮƽ����Ϊd=0.8m�ĵ÷���MIN�������Ϊ![]() ����ÿ��С�Ӹ����ɾ�ֹ�ͷţ�����ˮƽ��ļн�
����ÿ��С�Ӹ����ɾ�ֹ�ͷţ�����ˮƽ��ļн�![]() �ɵ����������ٶ�g=10m/s2����.
�ɵ����������ٶ�g=10m/s2����.

(1)С���뿪C��ʱ���ٶȶ��������ڵ÷�����N��?
(2)����N���С���ھ���C��ʱ�������С������������?
(3)��![]() ��ҪʹС�������ڵ÷������˵ij���L���ٵ��ڶ��٣�(��֪
��ҪʹС�������ڵ÷������˵ij���L���ٵ��ڶ��٣�(��֪![]() )
)
���𰸡���1��3m/s��2��1.25N��3��2.0m
�����������������(1)��ƽ���˶���֪ʶ��ˮƽ����ֱ�����з��̼�����⣻(2)��Բ���˶�![]() ���������ݼ�����⣻(3)����С��Ҫ���ڵ÷���С���C����ٶ����ɶ��ܶ�������⡣
���������ݼ�����⣻(3)����С��Ҫ���ڵ÷���С���C����ٶ����ɶ��ܶ�������⡣
(1) С���뿪C��ʱ��ƽ���˶������У� ![]() ��
�� ![]() ����������ʽ���
����������ʽ���![]() ��
��
(2) ������С�����������СΪF������C���У� ![]() �����
�����![]() ��
��
(3) С������M�㣬����C����ٶ�Ϊ�� ![]() ������С��Ҫ���ڵ÷���������C����ٶȴ�С��ΧΪ��2m/s��vC��3m/s����С���ͷŻ���C�㣬���ݶ��ܶ����ã�
������С��Ҫ���ڵ÷���������C����ٶȴ�С��ΧΪ��2m/s��vC��3m/s����С���ͷŻ���C�㣬���ݶ��ܶ����ã� ![]() �������ϸ�ʽ��ã�
�������ϸ�ʽ��ã� ![]()
���磺�������ؼ���������Ҫ���ڵ÷���С���C����ٶȣ����ɶ��ܶ�����⡣

 ����5��2���ϵ�д�
����5��2���ϵ�д�