Question

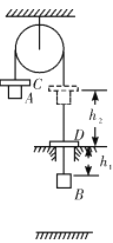
【题目】如图所示，高为h的光滑三角形斜劈固定在水平面上，其与水平面平滑对接于C点，D为斜劈的最高点，水平面的左侧A点处有一竖直的弹性挡板，质量均为m的甲、乙两滑块可视为质点，静止在水平面上的B点，已知AB＝h、BC＝3h，滑块甲与所有接触面的摩擦均可忽略，滑块乙与水平面之间的动摩擦因数为μ＝0.5.给滑块甲一水平向左的初速度，经过一系列没有能量损失的碰撞后，滑块乙恰好能滑到斜劈的最高点D处，重力加速度用g表示．求：

(1)滑块甲的初速度v0的大小；

(2)滑块乙最终静止的位置与C点的距离．

Answer 1

【答案】(1) ；(2)2h

【解析】试题分析：两个滑块的质量相等，发生的是弹性碰撞，碰后两者交换速度．根据能量守恒定律求滑块甲的初速度v0的大小；对整个过程，运用动能定理求出滑块乙在水平面上滑行的总路程，再得到乙最终静止的位置与C点的距离。

(1)由于滑块甲、乙碰撞时无能量损失，根据能量守恒定律得

甲、乙碰撞时根据动量守恒定律得

由以上两式解得

即滑块甲、乙碰撞的过程中速度互换，且每次碰撞都发生在B点

由于滑块乙刚好滑到斜劈的最高点D处，则对滑块乙由B点到D点的过程，根据动能定理得

解得

(2)设滑块乙在B、C间运动的总路程为x，对滑块乙由B点开始运动到最终静止的过程，根据动能定理得

解得，滑块乙最终停在C点左侧与C点距离为2h