题目内容
【题目】如图所示,两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面,现将质量相同的两个小球(小球半径远小于碗的半径),分别从两个碗的边缘由静止释放,当两球分别通过碗的最低点时( )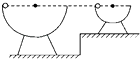
A.两球的动能相等
B.两球的加速度大小相等
C.两球对碗底的压力大小相等
D.两球的角速度大小相等
【答案】B,C
【解析】解:A、小球在运动过程中只有重力做功,机械能守恒,由机械能守恒定律得:EK=mgR,由于mg相同而R不同,则小球到达最低点时的动能不同,故A错误;
B、由机械能守恒定律得:mgR= ![]() mv2,在最低点,加速度a=
mv2,在最低点,加速度a= ![]() =2g,两球的加速度相等,故B正确;
=2g,两球的加速度相等,故B正确;
C、在最低点,由牛顿第二定律得:F﹣mg=m ![]() ,解得:F=3mg,球对碗底的压力F′=F=3mg,两小球对碗底的压力相等,故C正确;
,解得:F=3mg,球对碗底的压力F′=F=3mg,两小球对碗底的压力相等,故C正确;
D、小球的角速度ω= ![]() =
= ![]() ,由于两碗的R不同,则两球的角速度不变,故D错误;
,由于两碗的R不同,则两球的角速度不变,故D错误;
故选:BC.
两小球均只有重力做功,故机械能守恒,由机械能守恒定律可得出小球在碗底的动能和速度;由向心力公式可知小球对碗底的压力.

练习册系列答案
相关题目