题目内容
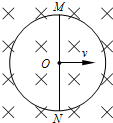 如图所示,把总电阻为2R的均匀电阻丝焊接成一半径为a的圆环,水平固定在竖直向下的磁感应强度为B的匀强磁场中,一长度为2a,电阻等于R,粗细均匀的金属棒MN放在圆环上,它与圆环始终保持良好的接触.当金属棒以恒定速度v向右移动经过环心O时,求:
如图所示,把总电阻为2R的均匀电阻丝焊接成一半径为a的圆环,水平固定在竖直向下的磁感应强度为B的匀强磁场中,一长度为2a,电阻等于R,粗细均匀的金属棒MN放在圆环上,它与圆环始终保持良好的接触.当金属棒以恒定速度v向右移动经过环心O时,求:(1)棒上电流的大小和方向及棒两端的电压UMN;
(2)在圆环和金属棒上消耗的总热功率.
分析:(1)由E=BLv求出感应电动势,由欧姆定律求出电流大小与棒两端电压,由右手定则可以判断出电流方向.
(2)由电功率公式P=UI可以求出电功率.
(2)由电功率公式P=UI可以求出电功率.
解答: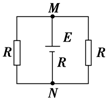 解:(1)导体棒运动产生电流,它相当于电源,内阻为R,
解:(1)导体棒运动产生电流,它相当于电源,内阻为R,
导体棒切割磁感线产生电动势:E=Blv=2Bav ①,
画出等效电路图如图所示,根据右手定则,
金属棒中电流从N流向M,所以M相当于电源的正极,N相当于电源的负极.
外电路总电阻为R外=
R ②,
根据闭合电路欧姆定律,棒上电流大小为:
I=
=
=
③,
棒两端电压是路端电压UMN=
?E ④
将数据代入④式解得:UMN=
Bav ⑤;
(2)圆环和金属棒上的总热功率为:P=EI ⑥,
由①⑥式解得:P=
⑦;
答:(1)棒上电流的大小为
,方向:从N流向M,棒两端的电压UMN=
Bav;
(2)在圆环和金属棒上消耗的总热功率为
.
 解:(1)导体棒运动产生电流,它相当于电源,内阻为R,
解:(1)导体棒运动产生电流,它相当于电源,内阻为R,导体棒切割磁感线产生电动势:E=Blv=2Bav ①,
画出等效电路图如图所示,根据右手定则,
金属棒中电流从N流向M,所以M相当于电源的正极,N相当于电源的负极.
外电路总电阻为R外=
| 1 |
| 2 |
根据闭合电路欧姆定律,棒上电流大小为:
I=
| E |
| R外+R |
| 2Bav | ||
|
| 4Bav |
| 3R |
棒两端电压是路端电压UMN=
| R外 |
| R外+R |
将数据代入④式解得:UMN=
| 2 |
| 3 |
(2)圆环和金属棒上的总热功率为:P=EI ⑥,
由①⑥式解得:P=
| 8B2a2v2 |
| 3R |
答:(1)棒上电流的大小为
| 4Bav |
| 3R |
| 2 |
| 3 |
(2)在圆环和金属棒上消耗的总热功率为
| 8B2a2v2 |
| 3R |
点评:本题是电磁感应与电学相结合的综合题,应用E=BLv、右手定则、欧姆定律、电功率公式即可正确解题.

练习册系列答案
相关题目
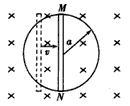
 如图所示,把总电阻为2R的一条粗细均匀的电阻丝焊接成直径为2d的圆环,与另一个直径为d的用绝缘材料制成的小环组成两个同心圆环,水平固定在绝缘桌面上.在小坏外部区域内穿过一个竖直向下,磁感强度为B的匀强磁场(小坏内部无磁场).长度为2d,电阻为R的粗细均匀的金属棒MN放在圆环上,与大圆环始终保持良好的电接触.当金属棒以恒定的速度v向右运动,经过环心O时,与大环的接触点为M和N,与小环的接触点为E和F.
如图所示,把总电阻为2R的一条粗细均匀的电阻丝焊接成直径为2d的圆环,与另一个直径为d的用绝缘材料制成的小环组成两个同心圆环,水平固定在绝缘桌面上.在小坏外部区域内穿过一个竖直向下,磁感强度为B的匀强磁场(小坏内部无磁场).长度为2d,电阻为R的粗细均匀的金属棒MN放在圆环上,与大圆环始终保持良好的电接触.当金属棒以恒定的速度v向右运动,经过环心O时,与大环的接触点为M和N,与小环的接触点为E和F.