Question

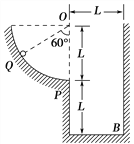
【题目】如图所示，质量mA＝0.8 kg、带电荷量q＝－4×10－3 C的A球用长l＝0.8 m的不可伸长的绝缘轻线悬吊在O点，O点右侧有竖直向下的匀强电场，场强E＝5×103 N/C.质量mB＝0.2 kg、不带电的B球静止在光滑水平轨道上，右侧紧贴着压缩并锁定的水平轻质弹簧，弹簧右端与固定挡板连接，弹性势能为3.6 J．现将A球拉至左边与圆心等高处由静止释放，将弹簧解除锁定，B球离开弹簧后，恰好与第一次运动到最低点的A球相碰，并结合为一整体C，同时撤去水平轨道．A、B、C均可视为质点，线始终未被拉断，不计空气阻力，g＝10 m/s2.求：

(1)碰撞过程中A球对B球做的功；

(2)碰后C第一次离开电场时的速度大小；

Answer 1

【答案】(1)－3.2 J　(2)4m/s

【解析】

（1）由题可得

mA＝mAgl

vA＝4 m/s

Ep＝ mB

vB＝6 m/s

以vA的方向为正方向，由动量守恒得

mAvA－mBvB＝(mA＋mB)vC

vC＝2 m/s

A对B所做的功

W＝mB－Ep＝－3.2 J

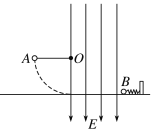
（2）碰后，整体C受到竖直向上的电场力

F＝|q|E＝20 N

G＝mCg＝10 N

因F－mCg>mC，整体C做类平抛运动

水平方向上：

x＝vCt

竖直方向上：

y＝at2

其中

a＝＝10 m/s2

圆的方程：

(y－l)2＋x2＝l2

解得：

x＝0.8 m

y＝0.8 m

C刚好在圆心等高处将轻线拉直，水平分速度变为零．此时C向上的速度为

v0＝at＝4 m/s

设C运动到最高点速度为v1,由动能定理得

mC－mC＝(F－mCg)l

v1＝4m/s