题目内容
8.火星探测器“勇气”号经过长时间飞行到达火星附近,成为一颗绕火星做圆周轨道运动的卫星.设“勇气”号距火星表面的高度为h,做匀速圆周运动的周期为T.已知火星的球体半径为R,引力常量为G.求:(1)火星的质量M;
(2)火星的密度ρ;
(3)火星表面的重力加速度g.
分析 (1)根据探测器的万有引力等于向心力列式求解即可;
(2)根据球体密度公式求解
(3)在火星表面,在不考虑自转的情况下,物体的重力等于万有引力
解答 解:(1)探测器的万有引力等于向心力,故:
G$\frac{Mm}{(R+h)^{2}}$=m($\frac{2π}{T}$)2(R+h)
解得:
M=$\frac{4{π}^{2}(R+h)^{3}}{G{T}^{2}}$
(2)密度$ρ=\frac{M}{\frac{4}{3}π{R}^{3}}$=$\frac{3(R+h)^{3}}{G{T}^{2}{R}^{3}}$
(3)由重力等于万有引力,有:
mg=m($\frac{2π}{T}$)2(R+h)
解得:
g=$\frac{4{π}^{2}(R+h)^{3}}{{T}^{2}}$
答:(1)火星的质量M为$\frac{4{π}^{2}(R+h)^{3}}{G{T}^{2}}$;
(2)密度$\frac{3(R+h)^{3}}{G{T}^{2}{R}^{3}}$
(3)火星表面的重力加速度g为$\frac{4{π}^{2}(R+h)^{3}}{{T}^{2}}$
点评 本题关键是明确探测器的向心力来源,根据牛顿第二定律列式求解,同时要注意在火星表面,重力等于万有引力,基础题目

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
1.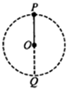 如图所示,与连接体固体的小球绕过O点的水平轴在竖直平面内做半径为r的圆周运动,图中P、Q分别为圆周的最高点和最低点,已知重力加速度为g,( )
如图所示,与连接体固体的小球绕过O点的水平轴在竖直平面内做半径为r的圆周运动,图中P、Q分别为圆周的最高点和最低点,已知重力加速度为g,( )
 如图所示,与连接体固体的小球绕过O点的水平轴在竖直平面内做半径为r的圆周运动,图中P、Q分别为圆周的最高点和最低点,已知重力加速度为g,( )
如图所示,与连接体固体的小球绕过O点的水平轴在竖直平面内做半径为r的圆周运动,图中P、Q分别为圆周的最高点和最低点,已知重力加速度为g,( )| A. | 若连接体是轻杆,小球到达P点的最小速度为$\sqrt{gr}$ | |
| B. | 若连接体是轻杆,小球在P点受到的轻杆的作用力可能为拉力,也可能为支持力,还可能为零,但在Q点,轻杆对小球只能为拉力 | |
| C. | 若连接体是轻绳,小球到达P点的速度可能为零 | |
| D. | 若连接体是轻绳,小球到达P点时受到轻绳的拉力可能为零 |
19.地球同步卫星到地心的距离r可由r3=$\frac{{a}^{2}{b}^{2}c}{4{π}^{2}}$求出,已知式中a的单位是m,b的单位是s,c的单位是m/s2,则( )
| A. | a是地球半径,b是地球自转的周期,c是地球表面处的重力加速度 | |
| B. | a是同步卫星轨道半径,b是同步卫星绕地心运动的周期,c是同步卫星的加速度 | |
| C. | a是赤道周长,b是地球自转周期,c是同步卫星的角速度 | |
| D. | a是同步卫星轨道半径,b是同步卫星运动的周期,c是地球表面处的重力加速度 |
3.一个矩形线框的面积为S,在磁感应强度为B的匀强磁场中,从线圈平面与磁场垂直的位置开始计时,转速为n rad/s,则( )
| A. | 线框交变电动势的峰值为$\sqrt{2}$nπBS | |
| B. | 线框交变电动势的有效值为nπBS | |
| C. | 从开始转动经过$\frac{1}{4}$周期,线框中的平均感应电动势为2nBS | |
| D. | 感应电动势瞬时值为e=2nπBSsin2nπt |
20.一个按正弦规律变化的交变电流的图象如图所示,由图可知( )


| A. | 该交变电流的有效值为10$\sqrt{2}$A | |
| B. | 该交变电流的最小值为-20A | |
| C. | 该交变电流的瞬时值表达式为i=20sin0.02t(A) | |
| D. | 该交变电流的频率为0.2 Hz |
17. 如图为杨氏双缝干涉实验示意图,其中S1、S2为双缝,D为光屏,实验中观察到屏上O点为中央亮纹的中心,P1为第一级亮纹的中心.在其他条件不变的情况下,若将D屏向右平移一段距离,则( )
如图为杨氏双缝干涉实验示意图,其中S1、S2为双缝,D为光屏,实验中观察到屏上O点为中央亮纹的中心,P1为第一级亮纹的中心.在其他条件不变的情况下,若将D屏向右平移一段距离,则( )
 如图为杨氏双缝干涉实验示意图,其中S1、S2为双缝,D为光屏,实验中观察到屏上O点为中央亮纹的中心,P1为第一级亮纹的中心.在其他条件不变的情况下,若将D屏向右平移一段距离,则( )
如图为杨氏双缝干涉实验示意图,其中S1、S2为双缝,D为光屏,实验中观察到屏上O点为中央亮纹的中心,P1为第一级亮纹的中心.在其他条件不变的情况下,若将D屏向右平移一段距离,则( )| A. | 屏上O点仍然为中央亮纹的中心 | B. | 屏上P1位置仍然可能为亮纹的中心 | ||
| C. | 屏上P1位置可能为暗纹的中心 | D. | 屏上干涉条纹间距将变小 |
18. 某人在竖直墙壁上悬挂一镖靶,他站在离墙壁一定距离的某处,先后将两只飞镖A、B由同一位置水平掷出,两只飞镖插在靶上的状态如图所示(侧视图),若不计空气阻力,下列说法正确的是( )
某人在竖直墙壁上悬挂一镖靶,他站在离墙壁一定距离的某处,先后将两只飞镖A、B由同一位置水平掷出,两只飞镖插在靶上的状态如图所示(侧视图),若不计空气阻力,下列说法正确的是( )
 某人在竖直墙壁上悬挂一镖靶,他站在离墙壁一定距离的某处,先后将两只飞镖A、B由同一位置水平掷出,两只飞镖插在靶上的状态如图所示(侧视图),若不计空气阻力,下列说法正确的是( )
某人在竖直墙壁上悬挂一镖靶,他站在离墙壁一定距离的某处,先后将两只飞镖A、B由同一位置水平掷出,两只飞镖插在靶上的状态如图所示(侧视图),若不计空气阻力,下列说法正确的是( )| A. | B镖的运动时间比A镖的运动时间长 | |
| B. | B镖掷出时的初速度比A镖掷出时的初速度大 | |
| C. | A镖掷出时的初速度与B镖掷出时的初速度一样 | |
| D. | A镖的质量一定比B镖的质量小 |
 在现代化的钢铁厂中,一般采用滚筒传送钢锭.如图所示为我国某钢铁厂的钢锭传送装置,斜坡长L=20m,高h=2m,斜坡上紧排着一排滚筒.长l=8m、质量m=1.0×103kg的钢锭ab放在滚筒上,钢锭与滚筒间的动摩擦因数μ=0.3,工作时由电动机带动所有滚筒顺时针匀速转动,使钢锭沿斜坡向上移动,滚筒边缘的线速度大小均为v=4m/s.由于斜坡倾角很小,可认为钢锭对滚筒的总压力近似等于钢锭的重力.取当地重力加速度g=10m/s2.
在现代化的钢铁厂中,一般采用滚筒传送钢锭.如图所示为我国某钢铁厂的钢锭传送装置,斜坡长L=20m,高h=2m,斜坡上紧排着一排滚筒.长l=8m、质量m=1.0×103kg的钢锭ab放在滚筒上,钢锭与滚筒间的动摩擦因数μ=0.3,工作时由电动机带动所有滚筒顺时针匀速转动,使钢锭沿斜坡向上移动,滚筒边缘的线速度大小均为v=4m/s.由于斜坡倾角很小,可认为钢锭对滚筒的总压力近似等于钢锭的重力.取当地重力加速度g=10m/s2.