题目内容
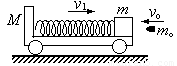
 质量为M=0.9kg的玩具小车静止在光滑的水平面上,小车的上表面是一光滑的曲面,末端是水平的,如图所示,小车被挡板P挡住,质量为m=0.1kg的小球从距地面高H=1米处自由下落,然后沿光滑的曲面继续下滑,小球落地点与小车右端水平距离s0=1米,取g=10m/s2,求
质量为M=0.9kg的玩具小车静止在光滑的水平面上,小车的上表面是一光滑的曲面,末端是水平的,如图所示,小车被挡板P挡住,质量为m=0.1kg的小球从距地面高H=1米处自由下落,然后沿光滑的曲面继续下滑,小球落地点与小车右端水平距离s0=1米,取g=10m/s2,求(1)小车右端距地面的竖直高度.
(2)若撤去挡板P,物体仍从原处自由落下,小球落地时落地点与小车右端水平距离是多少?
分析:(1)设小车右端距地面的竖直高度为h.小球从最高点下落至滑离小车时机械能守恒,由机械能守恒定律列式,则得h与平抛运动初速度的关系式;小球离开小车右端后做平抛运动,由平抛运动的规律列式得到高度h初速度的表达式,联立可求得h.
(2)去掉挡板时小球从最高点至离开小车之时系统机械能守恒,水平方向动量守恒.根据两大守恒列式求出小球离开小车时两者的速度.再根据平抛运动的规律求解.
(2)去掉挡板时小球从最高点至离开小车之时系统机械能守恒,水平方向动量守恒.根据两大守恒列式求出小球离开小车时两者的速度.再根据平抛运动的规律求解.
解答:解:(1)挡住小车时,设小球滑落时的速度v1,车尾部(右端)离地面高为h,小球从最高点下落至滑离小车时机械能守恒,则有
mg(H-h)=
m
,①
由平抛运动的规律得
s0=v1t ②
h=
gt2. ③
联立解得:h=0.5m,v1=
m/s
(2)设去掉挡板时小球离开小车时速度为v2,小车速度为v′2,小球从最高点至离开小车之时系统机械能守恒
mg(H-h)=
m
+
Mv
④
小球与小车相互作用过程中水平方向动量守恒 Mv′2-mv2=0. ⑤
此式不仅给出了v2与v′2大小的关系,同时也说明了v2是向右的.
得v2=
v1,v′2=
v2
代入解得 v2=3m/s,v′2=
m/s
小球离开车后对地平抛运动,则有
s2=v2t′⑥
h=
gt′2 ⑦
车在t′时间内向前的位移 s′2=v′2t′⑧
比较式⑦、③,得t′=t,解式①、④、⑤,得
此种情况下落地点距车右端的距离 s=s2+s′2=(
+v′2)t=(1+
)v2t=
v1t=s0
=1×
=
m.
答:
(1)小车右端距地面的竖直高度为0.5m.
(2)若撤去挡板P,物体仍从原处自由落下,小球落地时落地点与小车右端水平距离是
m.
mg(H-h)=
| 1 |
| 2 |
| v | 2 1 |
由平抛运动的规律得
s0=v1t ②
h=
| 1 |
| 2 |
联立解得:h=0.5m,v1=
| 10 |
(2)设去掉挡板时小球离开小车时速度为v2,小车速度为v′2,小球从最高点至离开小车之时系统机械能守恒
mg(H-h)=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| ′ | 2 2 |
小球与小车相互作用过程中水平方向动量守恒 Mv′2-mv2=0. ⑤
此式不仅给出了v2与v′2大小的关系,同时也说明了v2是向右的.
得v2=
|
| m |
| M |
代入解得 v2=3m/s,v′2=
| 1 |
| 3 |
小球离开车后对地平抛运动,则有
s2=v2t′⑥
h=
| 1 |
| 2 |
车在t′时间内向前的位移 s′2=v′2t′⑧
比较式⑦、③,得t′=t,解式①、④、⑤,得
此种情况下落地点距车右端的距离 s=s2+s′2=(
| v | 2 |
| m |
| M |
| M+m |
| M |
|
|
|
| ||
| 3 |
答:
(1)小车右端距地面的竖直高度为0.5m.
(2)若撤去挡板P,物体仍从原处自由落下,小球落地时落地点与小车右端水平距离是
| ||
| 3 |
点评:本题是机械能守恒、平抛运动、系统的动量守恒和机械能守恒的综合应用的问题,把握每个过程的物理规律是解题的关键.

练习册系列答案
相关题目
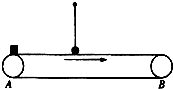 (2012?马鞍山模拟)如图所示,质量为m=0.9kg的物块无初速的轻放在皮带传送带的A端.皮带以速度v=5m/s匀逮运动.在距A端水平距离为3m处有一被细线悬挂的小球,刚好与皮带接触.细线长L=l.62m,小球的质量M=0.1㎏.已知皮带足够长,μ=0.5,(g取lOm/s2)
(2012?马鞍山模拟)如图所示,质量为m=0.9kg的物块无初速的轻放在皮带传送带的A端.皮带以速度v=5m/s匀逮运动.在距A端水平距离为3m处有一被细线悬挂的小球,刚好与皮带接触.细线长L=l.62m,小球的质量M=0.1㎏.已知皮带足够长,μ=0.5,(g取lOm/s2) (1)下列说法正确的是
(1)下列说法正确的是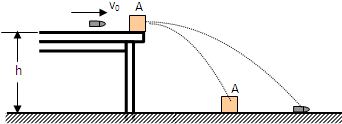 如图所示,在高为h=2.45m的光滑水平平台的边缘放着木块A,其质量为M=0.9kg,有一质量m=100g的子弹,以v0=500m/s的速度水平射穿木块A后,与A离开平台落到水平地面上(设射穿过程时间很短).测的子弹落地点到平台边缘的
如图所示,在高为h=2.45m的光滑水平平台的边缘放着木块A,其质量为M=0.9kg,有一质量m=100g的子弹,以v0=500m/s的速度水平射穿木块A后,与A离开平台落到水平地面上(设射穿过程时间很短).测的子弹落地点到平台边缘的