题目内容
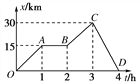
【题目】如图所示,在空间中取直角坐标系xOy,在第一象限内从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,MN为电场的理想边界,场强大小为E1,ON=d.在第二象限内充满一个沿x轴负方向的匀强电场,场强大小为E2.电子由第二象限的B点静止释放沿x轴负方向从y轴上的A点射入第一象限区域,且从MN上的P点离开.已知B点坐标为(-l,h).电子的电量为e,质量为m,电子的重力忽略不计,求:
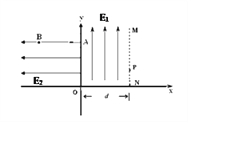
(1)电子从A点进入第一象限的速度大小;
(2)P点的坐标;
(3)电子经过x轴时离坐标原点O的距离.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:电子从A到B的过程做匀减速直线运动,根据牛顿第二定律求出加速度,再由速度公式求解时间;电子射入第一象限的电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,根据牛顿第二定律和运动学公式结合求解P点的坐标;电子离开电场后水平、竖直方向上都做匀速运动,先求出电子射出P点的速度,再由位移公式求解电子经过x轴时离坐标原点O的距离。
(1)从B到A的过程中,粒子加速度运动,由动能定理得:![]()
解得:![]()
(2)电子从A运动到P,做类平抛运动,则:
电子电场E1中的运动时间为:![]()
射出P点时竖直方向的分位移为:![]()
又根据牛顿第二定律得:![]()
联立解得:![]()
所以P点的坐标为(d,![]() )
)
(3)电子到达P点时,竖直分速度为:![]()
速度与竖直方向夹角θ,![]()
电子离开电场后水平方向有:△x=(h-y)tanθ
电子经过x轴时离坐标原点O的距离 x=d+△x=![]()

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】现代家庭电器化程度越来越高,用电安全是一个十分重要的问题.下表提供了一组部分人的人体电阻平均值数据,你认为下列说法正确的是( )
测量项目 | 干燥时电阻 | 出汗或潮湿时电阻 |
手与手之间 | 200 kΩ | 5 kΩ |
手与脚之间 | 300 kΩ | 8 kΩ |
脚与塑料鞋底之间 | 800 kΩ | 10 kΩ |
A. 从表中可看出干燥时的电阻是潮湿时的电阻的40~80倍
B. 对人体加220 V电压后,若对人的安全电流是22 mA以下,只有出汗或潮湿时是十分危险的
C. 对人体加220 V电压后,若对人的安全电流是22 mA以下,上述几项都十分危险
D. 从表中可看出干燥时对人体加220 V电压后的电流值最大是1.1 A