题目内容
质量为25kg的小孩坐在秋千板上，秋千板离拴绳子的横梁的距离为2m．如果秋千板摆动经过最低位置时的速度是2m/s，g取10m/s2．求：
（1）小孩在最低点时的加速度大小；
（2）最低点时小孩所受的支持力大小．
（1）小孩在最低点时的加速度大小；
（2）最低点时小孩所受的支持力大小．
分析：（1）秋千板摆动时，小孩做圆周运动，经过最低点时的加速度即为向心加速度，根据向心加速度公式a=
求出加速度．
（2）以小孩为研究对象，分析受力：在最低点时，小孩受到重力和板的支持力，由两个力的合力提供向心力，由牛顿第二定律求解支持力的大小．
| v2 |
| r |
（2）以小孩为研究对象，分析受力：在最低点时，小孩受到重力和板的支持力，由两个力的合力提供向心力，由牛顿第二定律求解支持力的大小．
解答：解：（1）由向心加速度公式得，孩在最低点时的加速度大小：a=
=
=2（m/s2）
（2）以小孩为研究对象，受力分析如图，可得：
F-mg=ma
即小孩所受的支持力大小：F=mg+ma=25×10+25×2=300 （N）
答：（1）小孩在最低点时的加速度大小是2m/s2；
（2）最低点时小孩所受的支持力大小是300N．
| v2 |
| r |
| 22 |
| 2 |
（2）以小孩为研究对象，受力分析如图，可得：
F-mg=ma
即小孩所受的支持力大小：F=mg+ma=25×10+25×2=300 （N）
答：（1）小孩在最低点时的加速度大小是2m/s2；
（2）最低点时小孩所受的支持力大小是300N．
点评：本题是生活中的圆周运动，掌握向心加速度的公式、分析向心力来源是求解的关键．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
相关题目
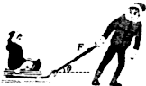如图所示，质量为25kg的小孩坐在5kg的雪橇上，大人用与水平方向成37°斜向上的大小为100N的拉力拉雪橇，使雪橇沿水平地面做匀速运动，（sin 37°=0.6，cos 37°=0.8，g=10m/s2）求：