题目内容
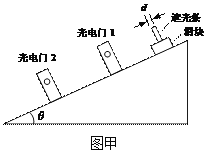
【题目】如图所示,倾角为37°的斜面固定在地面上,斜面的末端有一垂直于斜面的弹性挡板c,滑块与挡板c相碰后的速率等于碰前的速率,斜面上铺了一层特殊物质,该物质在滑块上滑时对滑块不产生摩擦力,下滑时对滑块有摩擦且动摩擦因数处处相同。现有一质量为M=0.9kg的滑块沿斜面上滑,到达最高点b时的速度恰好为零,此时恰好与从a点水平抛出的质量为m=0.1kg的小球在沿斜面方向上发生弹性碰撞,且滑块与弹性挡板c碰后恰好反弹回到b点。已知a点和b点距地面的高度分别为H=2.4m,h=0.6m(取g=10m/s2)。求:
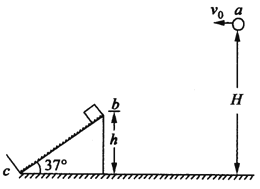
(1)小球做平抛运动的初速度大小;
(2)斜面与滑块间的动摩擦因数;
(3)从与小球碰撞到最后停止,滑块在斜面上通过的总路程。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】(1)小球从a到b做平抛运动,在竖直方向:![]()
小球到达b点时恰好沿斜面方向 ,有![]()
解得:![]() ;
;
(2)到达b点的速度![]()
小球与滑快发生弹性碰撞,由动量守恒定律得:![]()
由能量守恒定律得:![]()
解得滑块与小球刚碰后的速度![]()
由几何关系知斜面长![]()
滑块恰好反弹回到b点,由能量守恒定律得:![]()
解得:![]() ;
;
(3)设滑块与挡板第二次碰后到达最高点与c点的距离![]()
由能量守恒定律得:![]()
解得:![]()
设滑块与挡板第三次碰后到达最高点与c点的距离![]()
由能量守恒定律得:![]()
解得:![]()
以此类推![]()
所以滑块在斜面上共通过的路程为![]() 。
。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目