题目内容
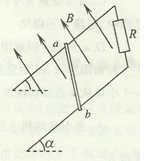
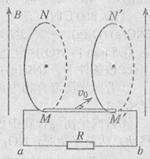
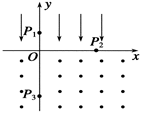
(18分)如图所示,在第一、二象限存在场强均为E的匀强电场,其中第一象限的匀强电场的方向沿x轴正方向,第二象限的电场方向沿x轴负方向。在第三、四象限矩形区域ABCD内存在垂直于纸面向外的匀强磁场,矩形区域的AB边与x轴重合。M点是第一象限中无限靠近y轴的一点,在M点有一质量为m、电荷量为e的质子,以初速度v0沿y轴负方向开始运动,恰好从N点进入磁场,若OM=2ON,不计质子的重力,试求:
(1)N点横坐标d;
(2)若质子经过磁场最后能无限靠近M点,则矩形区域的最小面积是多少;
(3)在(2)的前提下,该质子由M点出发返回到无限靠近M点所需的时间。
(1)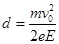 (2)S=
(2)S=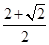
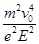 (3)T=2t1+t2=
(3)T=2t1+t2=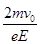 +
+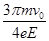
解析试题分析:(1)粒子从M点到N点做类平抛运动,设运动时间为t1,则有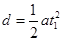 (1分)
(1分) 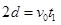 (1分)
(1分) 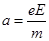 (2分)
(2分)
解得,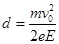 (2分)
(2分)
(2)根据运动的对称性作出质子的运动轨迹如图所示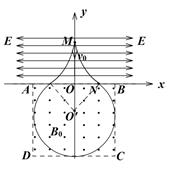
设粒子到达N点时沿x轴正方向分速度为vx,则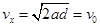 (1分)
(1分)
质子进入磁场时的速度大小为 (2分)
(2分)
质子进入磁场时速度方向与x轴正方向夹角为45o(1分)
根据几何关系,质子在磁场中做圆周运动的半径为R=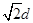 ,AB边的最小长度为2R=2
,AB边的最小长度为2R=2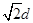 ,BC边的最小长度为R+d=
,BC边的最小长度为R+d=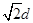 +d,矩形区域的最小面积为S=
+d,矩形区域的最小面积为S=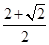
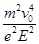 (2分)
(2分)
(3)质子在磁场中运动的圆心角为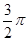 ,运动时间t2=
,运动时间t2=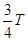 (1分)
(1分)
又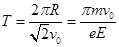 (2分)
(2分)
根据对称性,质子在第二象限运动时间与在第一象限运动时间相等,质子在第一象限运动时间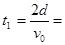
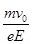 (1分)
(1分)
质子由M点出发返回M点所需的时间为:T=2t1+t2=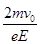 +
+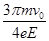 (2分)
(2分)
考点:带电粒子在复合场中的运动

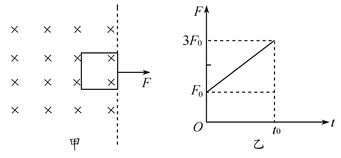
将金属块用压缩的轻弹簧卡在一个矩形箱子中,如图所示,在箱子的上顶板和下底板装有压力传感器,能随时显示出金属块和弹簧对箱子上顶板和下底板的压力大小。将箱子置于电梯中,随电梯沿竖直方向运动。当箱子随电梯以a=4.0m/s2的加速度竖直向上做匀减速运动时,上顶板的传感器显示的压力为4.0N,下底板的传感器显示的压力为10.0N。取g=10m/s2,若上顶板传感器的示数是下底板传感器的示数的一半,则升降机的运动状态可能是( )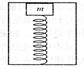
| A.匀加速上升,加速度大小为5m/s2 |
| B.匀加速下降,加速度大小为5m/s2 |
| C.匀速上升 |
| D.静止状态 |
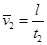 T,粒子的荷质比
T,粒子的荷质比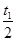 C/kg,不计粒子的重力。问:
C/kg,不计粒子的重力。问: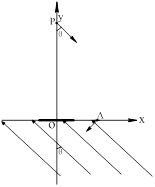
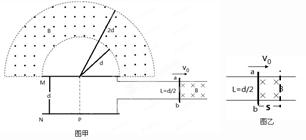
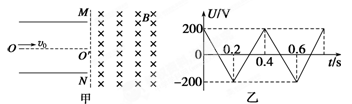
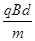 ,则为使粒子不从外圆飞出,则可以控制导轨区域磁场的宽度S(如图乙所示),那该磁场宽度S应控制在多少范围内
,则为使粒子不从外圆飞出,则可以控制导轨区域磁场的宽度S(如图乙所示),那该磁场宽度S应控制在多少范围内 ,轨道上端接一只阻值为R=0.4
,轨道上端接一只阻值为R=0.4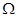 的电阻器,在导轨间存在垂直于导轨平面的匀强磁场,磁场的磁感应强度B=0.5 T,两轨道之间的距离为L=40cm,且轨道足够长,电阻不计。现将一质量为m="3" g,有效电阻为r=1.0
的电阻器,在导轨间存在垂直于导轨平面的匀强磁场,磁场的磁感应强度B=0.5 T,两轨道之间的距离为L=40cm,且轨道足够长,电阻不计。现将一质量为m="3" g,有效电阻为r=1.0