��Ŀ����
����Ŀ����ͼ��ʾ��ij�����轫����Ϊm�Ļ������Ϊ�ʵ㣩�Ӹߴ����������棬�����ù̶��ڵ������б������ͻ��ʹ�����ɹ���������ٻ��£������ˮƽ�����=37���ǣ������Ͻ�����������ŷ�������ȫ��ͬľ��A��B�����Ⱦ�Ϊl=2m����Ȳ��ƣ�������Ϊm��ľ���ϱ�������ĩ��ƽ�����ӣ���������б����䶯Ħ������Ϊ��0=0.125��������ľ��䶯Ħ������Ϊ��1��ľ�������䶯Ħ��������2=0.2���ش��������⣺�����Ħ�����뻬��Ħ������С��ȣ�sin37��=0.6��cos37��=0.8��g=10m/s2��

��1���������������h0=1.5m���ɾ�ֹ���£�����ﵽ����ĩ��ʱ���ٶ�v0��
��2�������ﻬ��ľ��Aʱ��ľ�岻����������ľ��Bʱ��ľ��B��ʼ����������1Ӧ�����������
��3������1=0.5��Ϊʹ����ǡ�ܵ���B�����Ҷˣ������ɾ�ֹ�»��ĸ߶�hӦΪ���٣�
���𰸡���1��1 5m/s����2��0.4����1��0.6����3��2.64m��
�������������������1����������б����ϵ�������ͼ����ţ�ٵڶ����ɣ� ![]()
�������ݽ��![]()
���˶�ѧ��ʽ�� ![]()
�������ݽ�ã� ![]()
��2��������ľ��Aʱ��ľ�岻����������������![]()
������ľ��Bʱ��ľ��B��ʼ������������������![]()
�����ܢ�ʽ�������ݵ�: ![]()
��3���ɣ�2��֪���ﻬ��Aʱ��ľ�岻����������ľ��Bʱ��ľ��B��ʼ������
�����»��߶ȼ�Ϊ![]() ������б��ĩ��ʱ�ٶȼ�Ϊ
������б��ĩ��ʱ�ٶȼ�Ϊ![]() ��
�� ![]()
���ﻬ��Aʱ���ȼ����˶������ٶȴ�Сa1=g��1=5m/s2
�����뿪Aʱ�ٶȼ�Ϊ![]() ��
�� ![]()
���ﻬ��Bʱ���������ٶȴ�С![]() ��
��
B�ļ��ٶȴ�С![]()
�����⣬���ﵽ��B���Ҷ�ʱ����ǡ�þ��й�ͬ�ٶȣ���Ϊ![]()
�������ȼ����˶��� ![]() ��
�� ![]()
B���ȼ����˶��� ![]() ��
�� ![]()
λ�ƹ�ϵ���㣺 ![]()
�������ݽ�ã� ![]()

 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�����Ŀ�������о������͵����쳤��ϵ��ʵ�飬�ⶨ���ɵľ���ϵ������һ������ˮƽ��һ�˹̶��ĵ��ɣ�����ļ��鵯��F�뵯�ɳ���L��Ӧ�������������ʾ��
F/N | 1.10 | 1.50 | 2.00 | 2.80 | 3.40 | 4.00 |
L/cm | 22.00 | 22.35 | 22.60 | 23.20 | 23.60 | 24.00 |
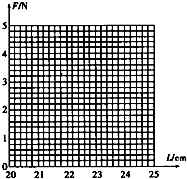
��1��������ͼ�������˵��ɵ�F��Lͼ�ߣ�
��2��F��Lͼ����L��Ľ���������ʾ��
��3�����ɵľ���ϵ��ΪN/m��
����Ŀ��ijͬѧ���ô���ʱ��̽��С���ٶ���ʱ��仯�Ĺ�ϵ�����ý������Ƶ��Ϊ50Hz��ͼ1Ϊij��ʵ���еõ���һ��ֽ����һ���֣�0��1��2��3��4��5��6��7Ϊ�����㣬�����������㻹��3�����δ��������ֽ���ϲ��x1=3.20cm��x2=4.74cm��x3=6.40cm��x4=8.02cm��x5=9.64cm��x6=11.28cm��x7=12.84cm

��1����ͨ�����㣬���±��ո�������ʵ����ݣ�������������λ��Ч���֣�
������ | 1 | 2 | 3 | 4 | 5 | 6 |
����������ٶȣ�ms��1�� | 0.50 | 0.70 | 0.90 | 1.10 | _________ | 1.51 |
��2�����ݱ������ݣ���ͼ2����������ϵ������v��tͼ����0��������Ϊ��ʱ��㣩����ͼ��ɵã�С���˶��ļ��ٶȴ�СΪ______m/s2��