题目内容
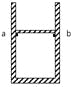
【题目】一个三棱柱由某种透明材料制作而成，为测量此材料折射率，现将三棱柱置于坐标纸上，如图三角形ABC为其横截面，顶点坐标为A(0，150mm)、B(-200mm，0)、C(200mm，0)。在纸上a、b两点插针，视线透过AC面观察a、b的像，并先后插上c、d两针使它们都挡住a、b的像。测得四针位置坐标a(-350mm，33mm)、b(-250mm，33mm)、c(200mm，99mm)、d(300mm，99mm)。
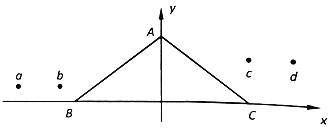
(ⅰ)请确定经过a、b的光线入射到BC面上时入射点的坐标；
(ⅱ)请计算此材料折射率。
【答案】(1) (-100mm , 0) (2) 
【解析】(ⅰ)根据题意做出光路如图，
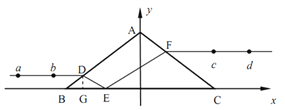
设光路在D点的入射角、折射角为
、
，在F点的入射角、折射角为
、
，由折射定律有
由几何关系
， 
又因△ABC为等腰三角形且∠B=∠C，可知△BDE∽△CFE，根据D、F纵坐标可得两三角形长度比例为
1:3，故BE=100mm，所以E点坐标为(-100mm,0)
(ⅱ)作DG⊥x轴，易求得BD=55mm，BG=44mm，GE=56mm，DE=65mm
从而可求得
， 
代入上面折射定律可得
练习册系列答案
相关题目
